Let us consider a linear model for intensity
![]() of the radio source in a point
of the radio source in a point ![]() on the observational
frequency
on the observational
frequency ![]() :
:
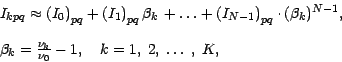
where ![]() is reference frequency corresponding to the
intensity
is reference frequency corresponding to the
intensity
![]() .
.
If the intensity ![]() in the point
in the point ![]() can be approximated
by power law as
can be approximated
by power law as

then we can present it as
where
![]() ,
,
and thus the spectral indexes
![]() can be obtained as
can be obtained as
Let us consider a target function
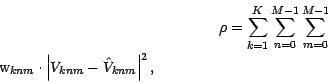
where,
![]() are weights,
are weights, ![]() ,
,
![]() is a measured and a model visibility function
respectively,
is a measured and a model visibility function
respectively,
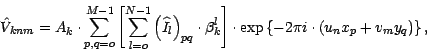
where, ![]() is a gain coefficient
is a gain coefficient
for k-th
antenna,
![]() is a normalized beam,
is a normalized beam, ![]() is a grid step.
is a grid step.
The problem of the optimization can be presented as a solution of the following system of linear equations:
for a vector of intensity
![]() , where the
, where the ![]() -th residual map
-th residual map
![]() can be defined as:
can be defined as:
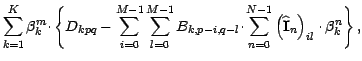 |
(1) | ||
| (2) |
where,
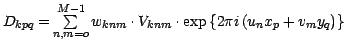 is a k-th
"dirty" map at the point
is a k-th
"dirty" map at the point
![]() ,
,
![$B_{k,p-i,q-l}=\sum\limits_{n,m=o}^{M-1}w_{knm}\exp \left\{ 2\pi i\left[
u_{n}\left( x_{p}-x_{i}\right) +v_{m}\left( y_{q}-y_{l}\right) \right]
\right\} $](img34.gif) is a k-th "dirty" beam at the point
is a k-th "dirty" beam at the point
![]() .
.
Let us choose the following initial conditions:
![]() for all
for all ![]() and
form
and
form
initial arrays
![]() and
and
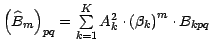 ,
, ![]() .
.
Calculation of the next s-th step (
![]() begins from the
choice of the point
begins from the
choice of the point ![]() , of the map maximum
, of the map maximum
Now it's possible to specify a vector
![]() :
:
and the residual maps
![]() :
:
Here
![]() is a positive defined
matrix of maximum values of weighted "dirty" beams,
is a positive defined
matrix of maximum values of weighted "dirty" beams,
![]() ;
; ![]() is a loop gain.
The process of the iteration can be completed if
is a loop gain.
The process of the iteration can be completed if
![]() , where
, where ![]() is a given accuracy.
Otherwise it is necessary to suppose
is a given accuracy.
Otherwise it is necessary to suppose ![]() and to calculate the next
and to calculate the next
![]() Conditions of the convergence of the
algorithm above is
Conditions of the convergence of the
algorithm above is ![]() ,
, ![]() .
.
The developed algorithm is nothing other than the
multi-frequency linear deconvolution, itself. this is described in
more detail this procedure by Likhachev, et al. (2003). Notice that the developed
algorithm allows to synthesize and analyze of high-quality VLBI images
directly from the visibility data measured on a few frequencies,
without analyses of the images itself. In case of multi-frequency linear
deconvolution, it is possible to synthesize an image of a radio source at any
intermediate frequency inside any given frequency band. Thus,
spectral interpolation of the image is feasible.
This part of the algorithm is carry out the synthesis
of the image itself. However, the algorithm also makes it possible to obtain an
estimate of the spectral index for a given radio source, i.e., it
implements the analysis of the image. It is clear
that multi-frequency imaging (MFI) will provide the highest angular
resolution possible for any VLBI project due to its improved
![]() -coverage.
-coverage.
The algorithm described above was implemented in the software, Astro Space Locator (ASL) for Windows (http://platon.asc.rssi.ru/dpd/asl/asl.html). It was developed by the Laboratory for Mathematical Methods of the Astro Space Center (Likhachev, 2003).
Fig.1 shows two deconvolved images of 3C84 as observed on the VLBA at 11 and 15 GHz respectively. Due to the better (u,v)-coverage, the quality and angular resolution of the interpolated MFS-image at 11 GHz is much better than for the same source at 15 GHz.
The authors thank Jon Romney (NRAO) for providing the observational data used in testing the new MFI algorithms.
Likhachev, S. F., Ladygin, V. A., & Guirin, I. A. 2003, Lebedev Phys. Institute Preprint, 31, 30p.
Likhachev, S. F.,Multi-Frequency Imaging for VLBI, Future Directions in High Resolution Astronomy, in print.