 |
Experience with these models shows that the predictive power in principle is so high that one can distinguish ``outliers'' into geometric effects (camera distortion, detector gridding), inaccurate entries in laboratory wavelength catalogues and insufficient description of the instrument proper on a scale below 0.1 of a spectral resolution element or pixel over fields many thousands of pixels across. At this point it is indispensable to be able to obtain the measurements of reference features in experimental data such as the wavelength calibration lines with a comparable intrinsic accuracy and repeatability.
It is obvious that the ultimate limitation for obtaining optimal calibration for differing modes of real instruments is the uncertainty associated with obtaining a ``true observed center'' for the calibration lines in the presence of noise. While ground based, visible wavelength calibration data usually can be exposed to have more than sufficient signal, space based observations are limited in exposure time by engineering constraints. HST STIS FUV MAMA wavelength calibration data in echelle mode with their typical low signal to noise ratios in the far UV are a particularly demanding case. An example of such data is shown in Figure 1, a 70 by 50 pixel window around two ``bright'' calibration lines (slit images) with a maximum photon count of 40 in the brightest pixel. The fainter line has a total of 875 counts spread over an area of 357 pixels.
As a reference case we used a STIS EG140H FUV MAMA mode 3000 sec long exposure, which contains some 700 identifiable lines from a Pt-Cr/Ne lamp in about 35 spectral orders between 1300Å and 1500Å, spread across a frame of 2000 by 2000 pixels. It is noteworthy that routine data for instrumental verification bracketing a typical science observation are typically exposed for 60 seconds only, i.e. a mere 2% of our study case.
In an iterative procedure the parameters of the STIS model have been carefully optimized for this mode to yield predictions of the line centers. The distribution of the residuals ``measured - predicted'' for these 700 line centers should yield a point symmetric cloud which, under ideal conditions, should be well centered around the origin and should assume a rather narrow distribution with a sigma corresponding to a fractional resolution element (line width) - in the present case about 0.2 pix.
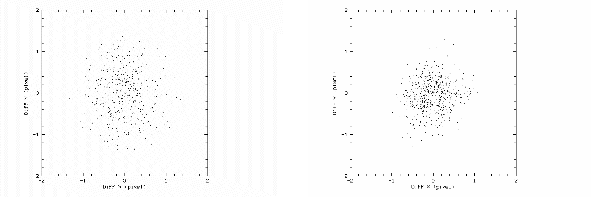 |
However, as can be seen in Figure 2 (left), the cloud is not really concentrated and has a characteristic size of 1 pixel. Naturally the question arises whether this reflects a ``weakness'' of the physical model, or the ``inability'' of the measurement procedure to ascertain the true observed line centers on the images instead.
As part of a collaboration between ESO/DMD/DFS and ST-ECF/IPMG groups we have evaluated object centering methods and verified that the ``measurements'' are obtained with the least amount of error and systematics can be excluded. Improvements in this area would benefit also to other data reduction steps based on line centering methods.
Initial starting point was the Feb 2003 version of the STIS-ANNEAL bundle from the STIS Calibration Enhancement project of the ST-ECF. Currently the baseline package utilizes the Levenberg-Marquardt (LM) method to fit a bi-dimensional Gaussian with six adjustable parameters (widths, amplitudes, angle between the two directions, background pedestal) to the data values in a selectable 2D-window around the estimated center of the feature (tilted and distorted monochromatic image of the slit).
It is clear that the lines (resp. slit images) in Figure 1 are NOT well described by two Gaussians. Therefore, finding a better model for the line shape offered an obvious route to improving the residuals between the STIS model and the actual measurements of line centroids. As shown in Figure 3 a bended, rotated, 2D-gaussoid looks more realistic. Unfortunately, the use of very complex analytical shapes in unattended fitting is very critical about the choice of starting values.
Thus we decided to limit the complexity of the line model by keeping some of the less important parameters fixed to appropriate values.
 |
These modifications allow a slight improvement of the line centroiding.
On the Web we located several different examples of implementations of the LM method (1D case). We searched the web for indications of limitations of the LM method in the presence of noise. Apparently the result of a fit is critically dependent on the choice of metric used to evaluate the goodness of the fit.
We analized several possibilities. Replacing in the chi-square criterium the sum of squares by the sum of the absolute distances one decreases the sensibility to outliers but also to the line wings improving the fit of line centers. But STIS data sets have often very extended lines with typically only ten photon counts in the centers. This makes very high the probability to have in the centers holes with very few or even no counts (Poisson-noise).
Taking into account the noise in the chi-square weighting factor one emphasizes those regions of the data window which by chance have less apparent shot noise. In the low signal domain of the present data that results in considerable "miscentering" even for relatively "bright" lines.
Finally we improved considerably the fit adopting a chi-square expression variant which is proportional to the inverse of the product between the measured data and the fitting function. This enforces a maximisation of the correlation between data and fit function shape. This modification is now being implemented as the default for the STIS-CE wavelength calibration baseline package. Figure 2 (right panel) shows the diagram of the residuals which should be compared to the starting conditions in Figure 2 (left panel).
In an attempt to understand the unexpected large residuals when comparing STIS FUV MAMA E140H echelle wavelength calibration images with the STIS-CE echelle model predictions we identified as the main source of error the inability of the fitting routines to provide accurate measurements of the noisy extended calibration lines.
Searching for remedies we tested a large number of modifications to the fitting algorithm and the fit model functions. We identified two successful modifications to the standard fitting package which is based on a Levenberg-Marquardt algorithm. We recommend to adapt the 2D line model from a simple bi-dimensional Gaussian to a gaussoid with different exponents in X and Y direction, which resemble the observed line profiles much better. We also recommend to modify the standard "chi-square" formula such that the correlation between the shapes of the line model and the line data is maximised.
Ballester, P., Rosa, M.R., 1997, A&A Suppl, 126, 563