ADASS 2003 Conference Proceedings

By constructing instrument models which incorporate as full as possible a knowledge of optical and detector physics, the calibration of astronomical data can be placed on a firmer footing than is currently the norm. A number of developments make it more practical today to efficiently use optical models in the whole observational process: At first, the proposer can prepare observations using model based exposure time estimators and data simulators. Second, the observatory controls the instrumental configuration, tests data analysis procedures and provides calibration solutions with the help of instrument and environment models. We show in particular how such models can be used to ease very significantly the calibration and operation of complex instruments from the Hubble Space Telescope and the Very Large Telescope and provide a high level of homogeneity and integrity in the post-operational archives. We review the role of instrument models for observatory operations, observing, pipeline processing and data interpretation and describe the current usage of instrument modelling at the ST-ECF and ESO.

1. Introduction

With ever more complex instruments entering service at general user type observatories an increasingly high importance is assigned to calibration tasks. The currently employed concepts for the calibration of observational data, evolutionary products of the historical development of instrument and detector technology, do not necessarily implement the best possible schemes to handle the precious data from large ground and space based facilities. Most of our calibration concepts are based on the principle of comparison with empirical readings from so called standards. Admittedly, computational tools have become much more elaborate, so that the standard readings (i.e. the calibration reference data) can be filtered and long term trends can be studied with the help of archives. However, at the very basis are empirical relations obtained from data containing noise. A typical example is the fitting of low order polynomials to obtain dispersion relations from wavelength calibration lamp spectra. The calibration strategies currently adopted in most of optical astronomy are empirical methods aimed at cleaning data from instrumental and environmental effects by a sequential application of instrumental corrections. Usually the transformation of detector based units into astrophysical units is done as a separate last step at the boundary between calibration and data analysis. The whole sequence makes it hard to arrive at a physical understanding of variations in instrumental characteristics which ought to drive maintenance measures or algorithmic solutions. It further requires a long learning process to determine the optimum deployment of resources - observing time for calibration observations and manpower for subsequent analysis.

The gap between the calibration of individual observations and the monitoring of instrument performance has been closed by new operational concepts such as the one designed for the VLT data flow (Haggouchi et al., 2004). But we need in addition to implement a physical calibration concept. As will be shown in the following, instrument models which provide the means to simulate the observational data gathering process from first principles form the basis for instrument configuration control, predictive calibration, and forward analysis. In this paper we review the use of instrument models at the Very Large Telescope (VLT) and the Hubble Space Telescope (HST) throughout the life-cycle of an observation: exposure time calculators for the VLT, first use of model based calibrations for the HST Faint Object Spectrograph, bootstrapping calibration of the VLT UV-Echelle Spectrograph, predictive calibration for the HST Space Telecope Imaging Spectrograph and finally controlling the performance of the VLT Interferometer.

2. Exposure Time Calculators

For the astronomer to be able to plan his observations, and for the Observation Programme Committee to be able to evaluate the quality of a proposed observation schedule, it is necessary to have good estimates of telescope performance and time required to reach the desired science objective. Exposure Time Calculators (ETCs) are one class of tools used to support this by modeling astronomical targets, telescopes and components in the optical path, and producing estimates of signal-to-noise ratios and exposure times. Some of the ETCs also provide information on the raw data products, such as simulated images and spectra or spectral formats. Furthermore, instrument scientists also use ETCs to evaluate the efficiency of instruments during the design phase. Moreover, ETCs may have a number of additional applications, for example for the estimation of limiting magnitudes in an archive environment (Voisin, 2004).

Exposure time calculators predict the observational performance of an instrument in terms of signal-to-noise reached or exposure time needed for a given target and under certain conditions. At the VLT we record since 1998 an increasing usage of such models from an initial value of 20 simulations per proposal to the present figure of 40 to 50. Peak usage takes place during the few days before the proposal deadline and can reach a total of 3000 a day. For this reason the ETC models are primarily designed for speed and easy maintenance, and less emphasis is placed on the accuracy of detail.

We provide centralised access from a single Web address and through a system of templates provide a homogeneous interface across the instruments. User interface templates, macro language, components database and configuration files, as well as the design of generic models facilitate the traceability and the maintainability of the system. We also cover the complete range of instrumentation at the VLT by supporting more than 25 instruments. These are not independent models, but rather six main programs for the optical imaging and spectroscopy, infrared imaging and spectroscopy as well as echelle and adaptive optics modes.

The ETCs rely on a variety of components, such as the transmissions and detector performance, and many specialised models are involved for the performance of adaptive optics systems, fiber optics or atmospheric sky emission. The accuracy of these models is about 10%. The engineering database contains laboratory measurements of the optical components. The level of accuracy is adequate for the preparation of observations given the fact that the actual realisation of observation conditions, intensity of atmospheric lines, level of continuums, seeing reached will produce a variability of the observing results. Exposure time calculators provide a first level of verification of the performance of an instrument if compared to measured performance.

3. Model-based Calibration for the HST Faint Object Spectrograph

In order to use models for data calibration, we need to reach a better accuracy than that of observation preparation models. Instrument models which are based on first principles clearly have the predictive power required to make substantial progress in the areas of calibration and data analysis. Before implementing the concepts of predictive calibration and model-based analysis, two central questions have to be answered.

3.1 Scattered Light Model

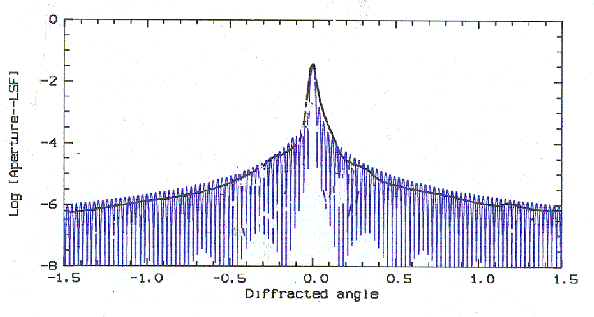
A first application of such modeling has been the FOS Scattered Light correction: calibrated UV spectra of a variety of targets show an unphysical upturn at the shorter wavelengths. The effect is much more pronounced for intrinsically red energy distributions. It is obvious that the intrinsic UV properties of such targets can only be recovered via a software model that simulates to a precision of better than one part per million the dispersion and image formation of the aperture-collimator-grating-detector combination. A physical model of the FOS, cast into software, was finally capable of correctly predicting the scattered light for any kind of intrinsic spectrum in all modes of the instrument (Bushouse, Rosa, Mueller, 1995). This model correctly replicates the relevant reflection, diffraction, dispersion and detection processes in the optical train of the FOS, and shows that the ultimate source of the scattered light are the far wings of the line spread function. The shape and level of these predicted far wings are very similar to the LSF measured pre-flight in the laboratory, indicating that the effect is not simply due to a deterioration of surfaces or adjustments. In fact the LSF is very close to the theoretical case of superb optics (Fig. 1), and only very small amounts of surface roughness and dust are required to explain the actual profile.

**Figure 1:** Line profile with extended wings of the HST FOS high resolution mode. The thick line is the actual laboratory pre-flight measurement while the undulating thin line is the prediction from the FOS optical model with unlimited spatial resolution
$\begin{figure} \plotone{O5-1_1.ps} \end{figure}$

This example demonstrates that a software model going beyond a simple throughput calculation, i.e. correctly describing all relevant physical effects, can be very powerful in solving problems encountered during the scientific analysis of data. Used in this way, the model appears simply as an additional data analysis tool in support of the calibration process. Ultimately, the goal is to go one step further and to advance from the calibration strategy of signature removal currently in use.

3.2 Dispersion Relation and Geomagnetic Image Motion

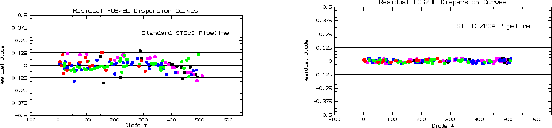
Another model could be successfully developed and applied to FOS data. The dispersion relation from the standard FOS pipeline was represented by a polynomial solution. The usual problem with polynomial solutions is that outliers and misidentifications will be included in the polynomial solution and make it converge away from the true solution. Instead, using a dispersion model based on the grating equation and the S-distortion model of the detector yield a substantial improvement of the calibration accuracy (Fig. 2).

**Figure 2:** Residuals of measured line positions with respect to the predicted location when using the standard FOS pipeline polynomial dispersion solutions (left panel), and when using the optical model based solutions of the POA-FOS pipeline (right panel)
$\begin{figure} \plottwo{O5-1_2a.ps}{O5-1_2b.ps} \end{figure}$

Since the FOS on HST used detector systems (Digicons) with electron optics, the observations were affected by the geomagnetic field. Insufficient magnetic shielding of these detectors resulted in an imprint of the changing geomagnetic environment during HST orbiting the earth onto the raw data - the so called geomagnetically induced image motion problem (GIMP). It had been identified early on after launch and an on-board correction had been applied to all observations from April 1993 onwards. However this correction itself was inadequate. As part of the Post-Operational Archive project (Rosa, 2000) of the ST-ECF both, the original effect and the inadequate procedure were modelised to yield an optimal correction for all 24000 measurements in the FOS archive at once.

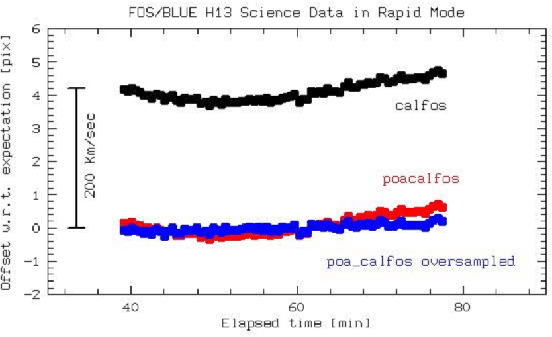
After correcting for the dispersion relation and the GIMP, a very substantial improvement of the radial velocities measurements could be obtained (Fig. 3). What was initially believed to be a grating wheel repeatability error turned out to be residual from an inadequate procedure that could only be proven and corrected through the physical model based approach (Rosa, Alexov, Bristow, Kerber, 2001)

**Figure 3:** Physical model based correction to a FOS science exposure: wavelength zero-point offsets in the original data (black symbols) and two versions of the model based correction (red and blue symbols) on a rapid-readout dataset spanning some 40 minutes of exposure time. More details are given in the above reference Rosa et al., 2001
$\begin{figure} \plotone{O5-1_3.ps} \end{figure}$

4. Predictive Calibration for the VLT UV-Echelle Spectrograph

If the model based approach proves to be useful for a low resolution first order spectrograph, we should consider to calibrate much more complex instruments. One of the most demanding cases of data calibration and analysis are 2D echelle spectra. Traditionally, they require complex data reduction procedures to cope simultaneously with both, the geometrical distortion of the raw data introduced by order curvature and line tilt, and with the spread of the signal across the tilted lines and between successive orders respectively. Unsupervised wavelength calibration for these instruments can only be achieved by reducing to a minimum the information needed to start the calibration process. This requires the most efficient use of the a priori knowledge from the optical properties of the instrument under consideration.

A generic description of spectrographs based on first optical principles has been developed (Ballester & Rosa, 1997). It incorporates off plane grating equations and rotations in three dimensions in order to adequately account for line tilt and order curvature. This formalism was validated by confronting the models for actual spectrographs (CASPEC and UVES from ESO, and STIS from HST) with ray tracing results and arc lamp exposures.

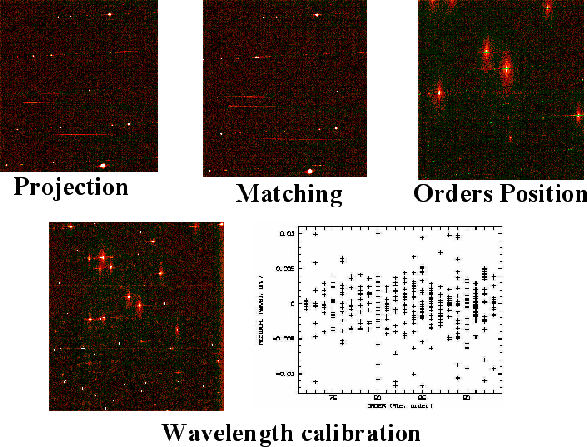
The geometric calibration is a complete definition of the spectral format including the order position and the wavelength associated to each detector pixel. This step was traditionally carried out via visual identification of a few lines and for this reason new methods had to be developed. The precision with which the geometric calibration is performed determines the accuracy of all successive steps, in particular the optimal extraction and the photometric calibration. In the case of UVES, the high non-linearity of the dispersion relation made it necessary to develop a physical model of dispersion in order to predict the dispersion relation and to efficiently calibrate the several hundreds of optical configurations offered by the instrument (Fig. 4).

**Figure 4:** Sequence of events during UVES geometric pipeline calibration. Model predicted positions of wavelength calibration lines are projected onto a format-check frame. The predicted positions are adjusted to the observed positions and an initial dispersion relation solution is produced. The order position is automatically defined on a narrow flat-field exposure using the physical model. The initial dispersion relation is refined on a Th-Ar frame in order to fully take into account the slit curvature
$\begin{figure} \plotone{O5-1_4.ps} \end{figure}$

To cover the many possible configurations the pipeline uses header information to select the appropriate optical layout. This layout is based on the specific knowledge of the optical design of the instrument, cast into a physical model. The model is involved at many stages of the calibration to provide reference values and initial solutions for the current configuration making the data reduction completely automatic. In addition to the calibration solutions, the pipeline delivers quality control information to assist the user in assessing the proper execution of the data reduction process. At the VLT this approach has been extended to other instruments, FLAMES-UVES which is a fiber adaptation of UVES, and also for the infrared ISAAC spectrograph where especially at the longer wavelength range there is a lack of atmospheric calibration lines (Yung, 2004).

5. The STIS Calibration Enhancement project

Since the benefits of using the 2D generic spectrograph model in the UVES pipeline have proved to be so essential for the quality and the repeatability of the science data, it was obvious to take the model based approach even further. The STIS/CE (Space Telescope Imaging Spectrograph Calibration Enhancement) project is a full fledged implementation of the physical model based approach for STIS on HST. The deliverables (ESA to NASA) involve the construction of a pipeline which is heavily based on first principles such as physical optics and CCD physics.

A major component of the STIS/CE pipeline is the STIS dispersion model, based on the formalism previously developed for UVES. In the case of STIS a mechanism is needed to optimize the configuration description of the instrument to an accuracy better than that provided by the engineering data, which can only be a starting point. There are fixed parameters precisely known from engineering such as number of grooves or focal lengths. Other parameters are not known to an accuracy sufficient for calibration purpose, for example grating angles. Finally some parameters may vary from exposure to exposure (repetition errors). Each mode is represented by a master configuration file that has been optimised using dedicated, long exposure time, calibration frames. From that individualised configuration files can be produced with the help of short exposures accompanying the science data. Currently the dispersion model predicts the location of wavelength catalog lines to a precision better than 0.1 pixel over an area of 2000x2000 pixels (Modigliani & Rosa, 2004). Paramount to this success was not only the refinement of the optical description, but also the re-measurement of wavelength calibration lamps at the National Institute of Standards and Technology (NIST) (Kerber, Rosa, Sansonetti, Reader, 2003).

Another interesting component of the STIS/CE pipeline is the corrective module for Charge Transfer Efficiency (CTE). The Charge Coupled Devices (CCDs) operating in hostile radiation environments suffer a gradual decline in their CTE, or equivalently, an increase in charge transfer inefficiency (CTI). STIS and WFPC2 have both had their CTE monitored during their operation in orbit and both indeed show a measurable decline in CTE that has reached a level that can significantly affect scientific results. As part of the Instrument Physical Modelling Group effort to enhance the calibration of STIS a model was developed of the readout process for CCD detectors suffering from degraded charge transfer efficiency. This model is based on simulating on the microscopic (single electrons) level the transfer of charge across the CCD chip during readout, and the trapping of electrons in defects of the silicon lattice. The model enables one to make predictive corrections to data obtained with such detectors (Bristow, 2004).

6. Models for the VLT Interferometer

With a maximum baseline length of 202 metres, the VLT Interferometer makes it possible to reach high angular resolution of the order of a few milliarcseconds. In March 2001, first fringes have been obtained with the VLT Interferometer using the test instrument VINCI. Three more instruments will be active at the VLT Interferometer, providing capabilities for coherent combination in the mid-infrared wavelength domain with MIDI, up to three near-infrared optical beams with AMBER, and simultaneous interferometric observations of two objects with PRIMA.

Preparing an interferometric observation requires adequate tools that can handle the geometrical configuration of the array and target/calibrator positions. Most observations in interferometry will involve measurements for different spatial frequencies and are likely to require different configurations and spread over extended periods of time, several weeks or several months. The geometrical constraints on the observation of the science and calibrator targets and the limited observability of the objects due to both the range of delay lines and shadowing effects will make it necessary to assess the technical feasibility of observations at both stages of phase 1 and phase 2 preparation. During phase 1, general tools like the WEB-based visibility calculator and exposure time calculators will be provided. In phase 2, the details of the observation can be validated more accurately.

The VLTI Visibility Calculator (Fig. 5) is the tool used for such calculations. The VLTI Visibility Calculator computes the fringe visibility as a function of the object diameter, the position of the target in the sky at the time of the observation, and the selected configuration. It takes into account the horizon map of the observatory and shadowing effects induced by telescope domes and structures on the observatory platform. It computes the optical path length, the optical path difference, and takes into account the range of the Delay Lines to estimate the period of observation for a given target. A second tool, the VLTI Calibrators Selection Tool, allows the user to query the list of VLTI calibrators and select the adequate targets for a given science object. With the longest VLTI baseline (202 m), angular resolutions can be measured at the scale of one milliarcsec (1 mas). Unresolved objects, namely objects much smaller than the 1 mas limit, will yield maximal visibility. The fringe visibility decreases with the angular size of the observed target.

We need also to understand the performance of the system and developed to this end a unified model of performance for the instruments of the VLT Interferometer. The commissioning instrument VINCI has been used for measurements for two years and the first science instrument MIDI has been commissioned in the course of 2003. The model predicts the accuracy on the visibility measurements. We are dealing here with new properties of the atmosphere, in particular one needs to characterise the atmospheric piston noise and its influence on the measurements. The predictions from this model are compared to the aggregated two years of VINCI measurements. Further verifications are now performed in the mid-infrared using MIDI measurements.

**Figure 5:** The VLTI Visibility Calculator and the Calibrators Selection Tool
$\begin{figure} \plotone{O5-1_5.ps} \end{figure}$

7. Conclusion

In conclusion, our ample experience with the physical model based approach allows us to address the questions that we raised at the beginning of this paper. Firstly, physical models can be developed, and they are accurate enough to solve many practical calibration problems in various operational environments (ground- and space-based). In particular, in several cases that we have described here, it would not have been possible to correct the data without a model. Today models are used in operations critical areas. The main additional benefit of models is that they provide an independent control on the data gathering process with the assurance that they are properly understood.

Acknowledgments

In this review we have tried to give credit to many contributors by citation of primary articles. It is clear that we could not include all of them and therefore would like to acknowledge also those contributions not mentioned explicitly in the text.

References

Bushouse, H., Rosa, M.R., Müller, Th. 1995, in ASP Conf. Ser., Vol. 77, Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes (San Francisco: ASP), p. 345

Kerber, F., Rosa, M.R., Sansonetti, C.J., Reader, J. 2003, ST-ECF Newsletter, 33, 2

Instrument Modelling in Observational Astronomy

Abstract: