The RASS x-ray data were largely analyzed with the Standard
Analysis Software System (SASS).
The results can be found in the Bright and Faint Source catalogues
(Voges et al. 1999, 2000).
Nevertheless, SASS is known for lack of sensitivity for faint or extended
sources.
This is due to the sliding window technique which locally
searches for count enhancements relative to the intensity in a
surrounding area defining the background intensity.
In multiple steps the window width is changed to allow for the detection
of extended sources.
But faint extended sources and blended faint sources in crowded fields
may get lost.
One reason is due to the local estimation of the background in a small
region around the
sliding window which may provide only poor signal-to-noise ratios (S/N).
The sources are characterized by fitting the candidate sources in a
further step using a Maximum-Likelihood (ML) method (Boese ![]() Doebereiner
2001).
The ML method works properly on prominent point-like sources which account for
94
Doebereiner
2001).
The ML method works properly on prominent point-like sources which account for
94![]() of the sources published in the RASS Bright Source catalogue.
The characteristics of the faint sources may not be properly estimated
in case of faint extended sources (Voges et al. 1999).
of the sources published in the RASS Bright Source catalogue.
The characteristics of the faint sources may not be properly estimated
in case of faint extended sources (Voges et al. 1999).
The present method using Bayesian Probability Theory (BPT) estimates the
background and sources in a single step neither employing pixel
censoring nor using a sliding window technique.
The aim is to infer simultaneously a background map for the complete field size
(
![]() in the sky) and a
probability for having source intensity in addition to the background
intensity in a pixel cell or pixel domain.
Bayesian inference allows reasoning on the basis of sparse data
employing additional information independent of the data.
The results are given by probability distributions quantifying our state
of knowledge.
For background estimation and source detection the additional
information is the assumption that the background is smooth, e.g. spatially slowly varying compared to source dimensions.
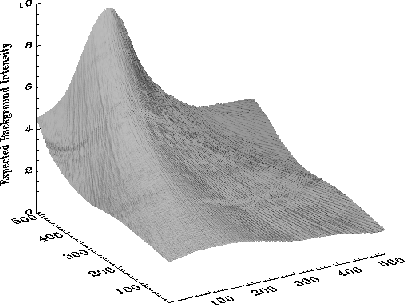
To allow for smoothness the background is modelled with a bivariate Thin-Plate spline.
The coexistence of background and sources is described with a probabilistic
two-component mixture model where one component describes
background contribution only and the other component describes
background plus signal contributions.
Each pixel cell (or pixel domain) is characterized by the
probability of belonging to one of the two mixture components.
For the background spline estimation the photons contained in all pixel cells
are considered including pixels containing additional source
contributions.
in the sky) and a
probability for having source intensity in addition to the background
intensity in a pixel cell or pixel domain.
Bayesian inference allows reasoning on the basis of sparse data
employing additional information independent of the data.
The results are given by probability distributions quantifying our state
of knowledge.
For background estimation and source detection the additional
information is the assumption that the background is smooth, e.g. spatially slowly varying compared to source dimensions.
To allow for smoothness the background is modelled with a bivariate Thin-Plate spline.
The coexistence of background and sources is described with a probabilistic
two-component mixture model where one component describes
background contribution only and the other component describes
background plus signal contributions.
Each pixel cell (or pixel domain) is characterized by the
probability of belonging to one of the two mixture components.
For the background spline estimation the photons contained in all pixel cells
are considered including pixels containing additional source
contributions.
This technique is applied on a data sample coming from the ROSAT PSPC in Survey Mode (0.1-2.4 keV). The ROSAT exposure map and the observatory's point spread function have been properly accounted for.
Given the observed data set
![]() , where
, where
![]() expresses photon counts in a pixel cell
expresses photon counts in a pixel cell ![]() ,
two complementary hypotheses arise:
,
two complementary hypotheses arise:
Additional assumptions are that no negative values for signal and background amplitudes are allowed and that the background is smoother than the signal. This is achieved by modelling the background count rate with a bivariate Thin-Plate spline where the supporting points are chosen sparsely to ensure that sources can not be fitted. The spline fits the background component whereas count enhancements classify pixel (domains) with source contributions.
The likelihood distributions for the two hypotheses are
Because we do not know if a certain pixel contains purely background or
additional signal, the likelihood for the mixture model is
| (3) |
![\begin{displaymath}
p(d_{ij} \mid \overline{B}_{ij},b_{ij},\lambda) =
\frac{e^{\...
...(d_{ij}+1),b_{ij}(1+\frac{1}{\lambda})]}{\Gamma(d_{ij}+1)} %$\end{displaymath}](img25.gif)
The probability of having source contribution in pixel cells or
domains is
| (4) |
 |
 |
BPT allows to estimate background maps and to detect sources in a single step providing consistent uncertainties of background and sources. The source probability is evaluated for single pixels as well as for pixel domains to enhance source detection for weak and extended sources. The detection sensitivity is enhanced compared to SASS results because the full field of view is exploited for background estimation. An extensive comparison with SASS results is beyond the scope of the present paper and will be addressed in a forthcoming paper.
Boese, F. G. & Doebereiner, S. 2001, A&A, 370, 649
Boese, F. G. 2000, A&AS, 141, 507
Fischer, R. & Dose, V. 2002, AIPC, 617, 143
Fischer, R. Hanson, K. M. Dose, V. & von der Linden, W. 2000, PRE, 61.1152
Voges, W. et al. 2000, IAUC, 7432
Voges, W. et al. 1999, A&A, 349, 389
von der Linden, W. Dose, V. Padayachee, J. & Prozesky, V. 1999, PRE, 59.6527