Next: Source Detection with Bayesian Inference on ROSAT All-Sky Survey Data Sample
Up: Algorithms & Classification
Previous: Promises and Challenges in Automatic Pattern Recognition
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
Gray, A. G., Moore, A. W., Nichol, R. C., Connolly, A. J., Genovese, C., & Wasserman, L. 2003, in ASP Conf. Ser., Vol. 314 Astronomical Data
Analysis Software and Systems XIII, eds. F. Ochsenbein, M. Allen, & D. Egret (San Francisco: ASP), 249
Multi-Tree Methods for Statistics on Very Large Datasets in Astronomy
Alexander G. Gray, Andrew W. Moore
School of Computer Science, Carnegie Mellon University
Robert C. Nichol
Department of Physics, Carnegie Mellon University
Andrew J. Connolly
Department of Physics and Astronomy, University of Pittsburgh
Christopher Genovese, Larry Wasserman
Department of Statistics, Carnegie Mellon University
Abstract:
Many fundamental statistical methods have become critical tools for
scientific data analysis yet do not scale tractably to modern large
datasets. This paper will describe very recent algorithms based on
computational geometry which have dramatically reduced the
computational complexity of 1) kernel density estimation (which also
extends to nonparametric regression, classification, and clustering),
and 2) the
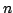
-point correlation function for arbitrary
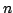
.
These new
multi-tree methods typically yield orders of magnitude
in speedup over the previous state of the art for similar accuracy,
making millions of data points tractable on desktop workstations for
the first time.
Statistical inference methods are a basic component of astronomical
research.
Nonparametric methods, in particular, make as few assumptions as possible
about the data's underlying distribution, and are thus of
particular relevance to scientific discovery in astronomy.
Unfortunately these tend to be much more
computationally intensive than parametric procedures.
In the era of massive and ever-growing astronomical databases, such as
the SDSS and several others, astronomical data analysis would seem to
have already surpassed the tractable regime of nonparametric methods,
which is roughly in the tens of thousands of data points on modern
desktop workstations. In this paper we summarize recent work in
computer science, in collaboration with astronomers and statisticians
(PiCA Group, www.picagroup.org) which has significantly extended
the ability of astronomers to perform nonparametric statistical
calculations with perfect or high accuracy on datasets of millions of
points and beyond.
A kd-tree records a 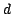 -dimensional data set containing
-dimensional data set containing 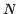 records.
Each node represents a set of data points by their bounding box.
Non-leaf nodes have two children, obtained by splitting the widest
dimension of the parent's bounding box. This crucial aspect of the
construction procedure makes this data structure adaptive to the
data distribution, unlike fixed grids or other simpler tree
structures. For the purposes of this paper, nodes are split until
they contain only one point, where they become leaves. An mrkd-tree
is a conventional kd-tree decorated, at each node, with extra
statistics about the node's data, such as their count, centroid, and
covariance. They are an instance of the idea of `cached sufficient
statistics' and are quite efficient in practice. mrkd-trees can be
built quickly, in time
records.
Each node represents a set of data points by their bounding box.
Non-leaf nodes have two children, obtained by splitting the widest
dimension of the parent's bounding box. This crucial aspect of the
construction procedure makes this data structure adaptive to the
data distribution, unlike fixed grids or other simpler tree
structures. For the purposes of this paper, nodes are split until
they contain only one point, where they become leaves. An mrkd-tree
is a conventional kd-tree decorated, at each node, with extra
statistics about the node's data, such as their count, centroid, and
covariance. They are an instance of the idea of `cached sufficient
statistics' and are quite efficient in practice. mrkd-trees can be
built quickly, in time
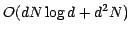 , where
, where 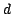 is the
dimensionality.
is the
dimensionality.
Figure 1 shows an mrkd-tree as well as simple
examples of two mechanisms which can be used to reduce computation.
Two basic prototype problems in computational geometry are that of
range-searching, or finding all points within radius  of a query
point
of a query
point
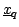 , and range-counting, in which the task is to simply
return the number of such points. By using the bounding boxes of
subsets of the dataset associated with nodes in the tree, we can
exclude all of these subsets from further exploration, i.e.recursive
traversal down the appropriate subtrees. This is called
exclusion pruning. In range-counting, we can additionally perform
inclusion pruning, since we have stored the node counts as sufficient
statistics. More complex forms of pruning are necessary for other problems.
, and range-counting, in which the task is to simply
return the number of such points. By using the bounding boxes of
subsets of the dataset associated with nodes in the tree, we can
exclude all of these subsets from further exploration, i.e.recursive
traversal down the appropriate subtrees. This is called
exclusion pruning. In range-counting, we can additionally perform
inclusion pruning, since we have stored the node counts as sufficient
statistics. More complex forms of pruning are necessary for other problems.
Figure 1:
An mrkd-tree. (a) Nodes at level 3. (b) Nodes at level
5. The dots are the individual data points. The sizes and positions
of the disks show the node counts and centroids. The ellipses and
rectangles show the covariances and bounding boxes. (c) The rectangles
show the nodes pruned during a range search for one (depicted) query
and radius. (d) More pruning is possible using range-counting instead of
range-searching.
|
|
Algorithms performing operations in a manner similar to that described
above have existed in computational geometry for some time. Problems
such as computing kernel density estimates and 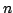 -point correlation
functions correspond to summations over pairs, triples, or in general
-point correlation
functions correspond to summations over pairs, triples, or in general
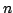 -tuples of points. We have developed a class of algorithms which
dramatically reduce the algorithmic complexity for such problems: it
is the extension of the previous single-tree methods to a new class we
call multi-tree methods (Gray, 2003). The first necessary element is the
extension of the previous point-node pruning mechanisms to analogous
node-node pruning mechanisms. This can be seen as a special
case of extending the general algorithmic device of divide-and-conquer
over a set to higher-order divide-and-conquer over
multiple sets.
-tuples of points. We have developed a class of algorithms which
dramatically reduce the algorithmic complexity for such problems: it
is the extension of the previous single-tree methods to a new class we
call multi-tree methods (Gray, 2003). The first necessary element is the
extension of the previous point-node pruning mechanisms to analogous
node-node pruning mechanisms. This can be seen as a special
case of extending the general algorithmic device of divide-and-conquer
over a set to higher-order divide-and-conquer over
multiple sets.
We first consider the method of kernel density estimation (KDE)
(Silverman 1986), a very widely analyzed and applied class of
nonparametric density estimation techniques. Analogous kernel
estimators exist for nonparametric regression, and KDE can be used as
a subroutine to construct nonparametric classification procedures and
clustering procedures. The task we consider in this paper is that of
computing the density estimate
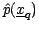 for each point
for each point
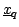 in
a query dataset containing
in
a query dataset containing 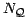 points, given a reference
dataset containing
points, given a reference
dataset containing 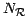 points and a local kernel function
points and a local kernel function
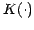 centered upon each reference datum and having scale
parameter
centered upon each reference datum and having scale
parameter  (the 'bandwidth'), or
(the 'bandwidth'), or  . The density
estimate at the
. The density
estimate at the
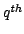 query point
query point
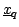 is
is
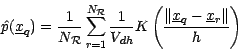 |
(1) |
where 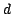 is the dimensionality of the data and
is the dimensionality of the data and
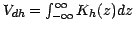 ,
a normalizing constant depending on
,
a normalizing constant depending on 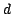 and
and  .
.
Note that two typical forms for the kernel function 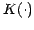 are the
spherical kernel (
are the
spherical kernel (
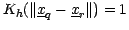 if
if
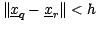 , otherwise
, otherwise 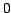 , with normalizing constant
, with normalizing constant 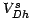 , the volume of
the sphere of radius
, the volume of
the sphere of radius  in D dimensions) and the Gaussian kernel.
The spherical kernel corresponds exactly to the range-counting problem
as described earlier, but because the Gaussian function does not have
finite extent, our previous notion of pruning must be extended to one
of approximation, which will not be described here for lack of space.
in D dimensions) and the Gaussian kernel.
The spherical kernel corresponds exactly to the range-counting problem
as described earlier, but because the Gaussian function does not have
finite extent, our previous notion of pruning must be extended to one
of approximation, which will not be described here for lack of space.
Figure 2:
Examples of experimental runtimes. (a) This shows the advantage of
dual-tree KDE over a single-tree implementation, on an SDSS sample in 2
dimensions (RA and Dec). Note the linear
growth in runtime for dual-tree KDE. Performed on a 1999-era Pentium
Linux workstation. Relative approximation error is less than 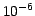 .
(b) Runtime for the 3-point correlation, on a mock
galaxy catalog based upon a Virgo Lambda CDM simulation in 3 dimensions.
Note that the computation is exact, not approximate.
Performed on a 2002-era Linux Pentium.
.
(b) Runtime for the 3-point correlation, on a mock
galaxy catalog based upon a Virgo Lambda CDM simulation in 3 dimensions.
Note that the computation is exact, not approximate.
Performed on a 2002-era Linux Pentium.
|
|
Point processes are stochastic processes whose realizations
consist of point events in space (or time, the one-dimensional case).
The Poisson process is the most basic and important point process
model. Poisson statistics thus form the foundation of spatial
statistics and have long formed a critical tool in astrophysics
(Peebles 1980). The 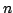 -point correlation function (
-point correlation function (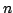 pcf)
corresponds to the
pcf)
corresponds to the  moment of Poisson counts. For
example the joint probability of finding points in each of the three
volume elements
moment of Poisson counts. For
example the joint probability of finding points in each of the three
volume elements 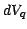 ,
, 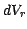 and
and 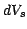 is given by
is given by
![\begin{displaymath}
dP = \lambda^3 dV_q dV_r dV_s [ 1 + \xi(\delta_{qr}) + \xi(\...
...xi(\delta_{sq}) + \zeta(\delta_{qr},\delta_{rs},\delta_{sq}) ]
\end{displaymath}](img25.gif) |
(2) |
where  ,
,  , and
, and 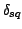 are the sides of the
triangle defined by the three points
are the sides of the
triangle defined by the three points
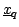 ,
,
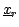 , and
, and
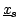 .
.
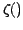 is called the reduced 3-point correlation function.
In general we refer to this quantity in place of the full correlation function
since it is what we need to concern ourselves with computationally.
is called the reduced 3-point correlation function.
In general we refer to this quantity in place of the full correlation function
since it is what we need to concern ourselves with computationally.
Computation of the 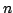 pcf can be viewed as a form of range-counting
problem: however here the problem is that of counting the number of
pcf can be viewed as a form of range-counting
problem: however here the problem is that of counting the number of
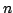 -tuples whose pairwise distances match a user-specified template
for the permissible ranges. The additional challenges posed by this
generalization from pairs (as in KDE) to
-tuples whose pairwise distances match a user-specified template
for the permissible ranges. The additional challenges posed by this
generalization from pairs (as in KDE) to 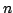 -tuples for arbitrary
-tuples for arbitrary 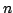 include the definition of an appropriate recursion strategy and
allowance of all possible permutations of the template
include the definition of an appropriate recursion strategy and
allowance of all possible permutations of the template 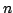 -gon. These
additional complexities will not be described here for lack of space.
-gon. These
additional complexities will not be described here for lack of space.
Figure 2 shows some typical examples of experimental
performance, ranging up to 1 million points. Further details,
including mathematical runtime analyses, can be found in (Gray &
Moore 2003, Moore et al. 2001) and journal papers to appear. We
anticipate that these algorithms will open the door to significant
astronomical analyses which could not have been suggested previously.
References
Friedman, J., Bentley, J., & Finkel, R. 1977,
ACM Trans. Math. Soft., 3, 3
Gray, A. G. 2003, CMU Computer Science Dept. PhD thesis
Gray, A. G. & Moore, A. W. 2003, in Proc. SIAM Int'l. Conf.
Data Mining, SIAM Press
Moore, A. W. et al. 2000, Proc. Mining the Sky, Springer-Verlag
Peebles, P. J. E. 1980, The Large-Scale Structure of the Universe,
Princeton University Press
PiCA (Pittsburgh Computational Astrostatistics Group),
www.picagroup.org
Silverman, B. W. 1986, Density Estimation for Statistics and
Data Analysis, Chapman and Hall/CRC
© Copyright 2004 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: Source Detection with Bayesian Inference on ROSAT All-Sky Survey Data Sample
Up: Algorithms & Classification
Previous: Promises and Challenges in Automatic Pattern Recognition
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
![]() of a query
point
of a query
point
![]() , and range-counting, in which the task is to simply
return the number of such points. By using the bounding boxes of
subsets of the dataset associated with nodes in the tree, we can
exclude all of these subsets from further exploration, i.e.recursive
traversal down the appropriate subtrees. This is called
exclusion pruning. In range-counting, we can additionally perform
inclusion pruning, since we have stored the node counts as sufficient
statistics. More complex forms of pruning are necessary for other problems.
, and range-counting, in which the task is to simply
return the number of such points. By using the bounding boxes of
subsets of the dataset associated with nodes in the tree, we can
exclude all of these subsets from further exploration, i.e.recursive
traversal down the appropriate subtrees. This is called
exclusion pruning. In range-counting, we can additionally perform
inclusion pruning, since we have stored the node counts as sufficient
statistics. More complex forms of pruning are necessary for other problems.
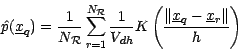
![]() are the
spherical kernel (
are the
spherical kernel (
![]() if
if
![]() , otherwise
, otherwise ![]() , with normalizing constant
, with normalizing constant ![]() , the volume of
the sphere of radius
, the volume of
the sphere of radius ![]() in D dimensions) and the Gaussian kernel.
The spherical kernel corresponds exactly to the range-counting problem
as described earlier, but because the Gaussian function does not have
finite extent, our previous notion of pruning must be extended to one
of approximation, which will not be described here for lack of space.
in D dimensions) and the Gaussian kernel.
The spherical kernel corresponds exactly to the range-counting problem
as described earlier, but because the Gaussian function does not have
finite extent, our previous notion of pruning must be extended to one
of approximation, which will not be described here for lack of space.
![]() pcf can be viewed as a form of range-counting
problem: however here the problem is that of counting the number of
pcf can be viewed as a form of range-counting
problem: however here the problem is that of counting the number of
![]() -tuples whose pairwise distances match a user-specified template
for the permissible ranges. The additional challenges posed by this
generalization from pairs (as in KDE) to
-tuples whose pairwise distances match a user-specified template
for the permissible ranges. The additional challenges posed by this
generalization from pairs (as in KDE) to ![]() -tuples for arbitrary
-tuples for arbitrary ![]() include the definition of an appropriate recursion strategy and
allowance of all possible permutations of the template
include the definition of an appropriate recursion strategy and
allowance of all possible permutations of the template ![]() -gon. These
additional complexities will not be described here for lack of space.
-gon. These
additional complexities will not be described here for lack of space.