ADASS 2003 Conference Proceedings

Pattern recognition is to identify and model regularities in empirical data by algorithmic processes. Successful application of the established methods requires good understanding of their behavior and how well they match a particular context. Difficulties can arise from either the intrinsic complexity of a problem or a mismatch of methods to problems. We describe our efforts in characterizing the intrinsic complexity of a classification problem and its relationship to classifier performance. We discuss how Mirage, an exploratory data analysis tool, is designed to help integrate domain expertise into the process of solution development.

Many large-scale sky surveys in progress or in planning are expected to generate data at a rate far beyond reach by traditional manual analysis. Inevitably some form of automatic analysis must be employed at a certain stage of the data processing pipeline. Ideally, automatic analysis should go beyond routine data reduction operations, and play an active role in assisting and accelerating the process of knowledge discovery.

Here astronomy shares similar concerns with many other areas of study, like weather forecasting, earth observation, robotic perception, medical diagnosis, security monitoring, web-based information retrieval, and financial engineering. There are similar needs for processing numbers, time series, images, sound, and spectral observations to extract useful information and detect new events. One may even argue that, the ability to recognize patterns from observations is at the heart of human intelligence. Besides these explicit applications, many of our daily activities like physical navigation, social interactions, and decision making, all depend critically on this ability.

Algorithmic methods for discovering regularities and irregularities in data sets have been under active research over the entire history of development in computing machinery. In some application domains there have been good progresses resulting in successful algorithms in routine use, such as in postal address reading machines for high-speed, large-volume mail sorting. But obviously we are still far from solving all potential application problems. In this article we review what have been accomplished in the methodology, and what challenges are ahead.

2. Essential Tasks and Methods in Automatic Pattern Recognition

The process of automatic pattern recognition involves several key tasks: choice of a good feature representation, design of procedures for feature extraction, selection of relevant features for classification, and from there it can go into supervised or unsupervised learning (Jain et al. 2000).

In supervised learning (discrimination), we use a labeled training set to tune a chosen classifier so that it can assign an unseen sample to one of the several pre-defined classes exemplified in the training set. This involves choosing a classifier (an algorithm among several known families), training the classifier (developing the necessary data structures or tuning the critical parameters), and evaluating the classifier to set expectation on its accuracy before the actual application. Success of the process is measured by the accuracy in class assignment on a new data set.

In unsupervised learning (clustering), there are no pre-defined classes. We need to choose and tune an algorithm to find clusters that are subsets of data sharing some common properties. This involves choosing and tuning a clustering algorithm, and evaluating the results within the application context. Good results are those satisfying a specific validation criterion associated with the algorithm, or those with useful interpretations in the context of the domain knowledge.

Feature Extraction and Representation

Feature extraction is the process of obtaining measurements of the objects. The measurements can come directly from sensor output, or can be reduced and refined by domain-specific algorithms or generic tools like Gabor analysis, Fourier analysis, wavelet analysis, or principle component analysis. Features need to be informative of the task at hand. This is where domain expertise can do most help: which shape features are the most critical descriptors of galaxy morphology? should a set of light curve be normalized by maximum intensity or by duration per cycle? is an object's position important for identification of its type? which coordinate system is the most appropriate for this task? A good set of features have strong impact on the success of the subsequent recognition process.

In representing the features there are several choices: (1) fixed length numerical vectors; (2) symbol strings; (3) graphs and other data structures. There is a depository of recognition methods matching each feature representation. In addition, there are rule-based classifier systems that can handle different kinds of feature representations. The rules can be hand-designed, deduced by formal logic, or selected by genetic algorithms.

Classifiers and Clustering Algorithms

Symbol strings are typically processed by syntactic pattern recognition methods. These methods represent each class by a grammar consisting of a set of allowed symbols and production rules. The classifier is a parser that tries to reduce the input string to the most likely generating symbol according to the production rules. Syntactic methods are best suited to problems with clear primitives and stable intermediate structures, with well defined and known alternatives. Domain knowledge can be explicitly encoded into the grammar (Trahanias & Skordalakis 1990). However, if good knowledge about the problem's structure is not available, automatically inferring the grammar from a sample set is a very difficult task.

Features represented by graphs are processed by structural methods like graph matching for isomorphisms, elastic matching, and subtree matching. Both the data structure and the matching procedure can encode knowledge about the problem. Careful heuristic designs are needed in most applications. Difficulties include how to build noise tolerance into the matching algorithms, and how to deal with the combinatorial complexity.

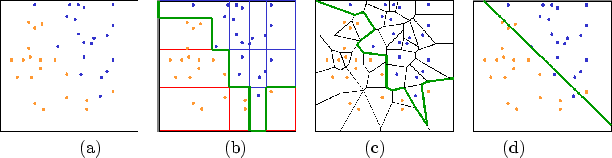
Fixed length numerical vectors are the most commonly used feature representations. Feature vectors are processed by statistical pattern recognition methods. Table 1 lists several major families of classification methods in this category. Statistical pattern recognition methods do not rely on explicit encoding of domain knowledge. The classifier training procedures include mechanisms for inferring the distribution of each class in the feature space. This makes them widely applicable, and they are by far the richest and the most successful category of methods in practice. However, even with a wide range of choices in classifier algorithms, there is no guarantee of success for any particular application. Often the difficulty is in finding the right method best suited for the problem at hand (Figure 1).

Table 1: Common methods for supervised classification.

method	principle	variants
Bayesian classifiers	estimate the class-conditional distribution using the training samples; assign an unknown sample to the class with maximum a posteriori probability	(1) parametric procedures: estimates of probability distributions are based on an assumed functional form (e.g. Gaussian); (2) nonparametric procedures: no functional form of the distributions is assumed; the empirical distributions are described using generic estimators (e.g. based on kernels) or low-order approximations based on weak assumptions such as continuity and smoothness
linear classifiers	infer a hyperplane best separating two classes (or each class from the rest); assign an unknown sample to the side of the hyperplane believed to contain its class	(1) many variations in the procedure of inferring the hyperplane: Fisher's discriminant analysis, equi-distance divider between class means (nearest mean classifier), minimizing sum of error distances, maximizing margins, or by iterative weight adjustments minimizing errors. (2) by applying nonlinear transformations on the original features, the problem can be embedded in a new space where a linear classifier can describe a nonlinear boundary in the original space (as in support vector machines)
nearest neighbor classifiers	assign an unknown sample to the class represented by training samples in its vicinity	(1) variations by the distance metric; (2) K-nearest neighbors: take votes from the classes of several nearest neighbors; (3) reduced, condensed classifiers where only a subset of the training samples are used, mostly for efficiency concern
decision trees & forests	construct a tree representing a hierarchical partitioning of the feature space into leaves where a single class dominates; propagate an unknown sample down the tree to a particular leave node and assign it to the class with maximum probability at the leave node	(1) variations by the type of split at each internal node; (2) variations by the algorithm for tree construction: how features and their weights are chosen at each split, when to stop growing the tree, whether the tree is pruned back for better generalization power; (3) decision forests: voting by an ensemble of decision trees, each tree differing in training samples or subsets of features used
neural networks	design and weigh connections between groups of source, target, and intermediate nodes representing hidden structures; propagate an unknown sample through the network until it reaches the target group, threshold or take maximum of accumulated scores to decide on its class	(1) architectural variations: multi-layer perceptrons, radial basis networks, Hopfield nets, learning vector quantization; (2) differences in several aspects of the training procedure: target function for optimization, algorithm for weight adjustment, validation procedure for termination of training, and network size control
ensemble methods	train a committee of classifiers together with a decision combination rule; feed an unknown sample to each component classifier and combine their decisions on its class	(1) variations in the ensemble size and the mixture of classifier types; (2) differences in the procedures for constructing and optimizing the ensemble (3) variations in the decision combination rules

For unsupervised learning there are also a large collection of algorithms, including parametric methods like mixture estimation (most commonly Gaussian mixtures), and nonparametric methods like the k-means algorithm, mode seeking procedures (finding density peaks or valleys), self-organizing maps (a neural network), graph based methods (minimal spanning tree), and hierarchical methods. Many of these methods have found good uses in some problems. However, like in supervised learning, matching the methods to problems still presents major difficulty, since each method has certain implicit assumptions about the data distributions. Coupled with the lack of an absolute notion of correctness, success in unsupervised learning is often difficult to determine.

The uncertainty in matches between methods and problems reduces the application of learning algorithms to a lengthy trial-and-error process, which is far from desirable for processing large surveys where many potential questions can be formulated on the combinatorial interactions of many parameters. The uncertainty is rooted in a lack of understanding on how data distributions interact with classifier geometry and the sampling processes. We believe that the key to improve upon the current level of automation in pattern learning is a better understanding of data set complexity in high-dimensional spaces, especially, the geometry of data distributions and its detailed relationship to classifier behavior. In the next section we describe some of our recent studies along these lines.

**Figure 1:** Class boundary according to different classifiers: (a) an example two-class, two-dimensional problem; class boundary according to (b) XCS classifier (a genetic algorithm), (c) nearest-neighbor classifier, and (d) a linear classifier.
$\begin{figure} \epsscale{.22} \centering\begin{tabular}{cccc} \plotone{O3-1_f1a.... ....85in} (b) & \hspace{0.8in} (c) & \hspace{0.8in} (d) \end{tabular}\end{figure}$

3. Characterization of Data Complexity by Geometrical Measures

Given an arbitrary discrimination problem, how do we know whether it is intrinsically solvable by the automatic methods? Given an arbitrary clustering problem, how do we know whether there are indeed distinct clusters and which algorithm has the best chance of finding them? If we do not expect distinct classes, how do we recognize other types of regularities, such as a trend in evolution, a specific trajectory in a state space, a compact, low-dimensional distribution in a high-dimensional feature space? How can we find out about any irregularities that may indicate new facts? How do we do all these if the patterns may be buried among irrelevant data and measurements?

To answer many of these questions it requires a detailed understanding of how the data are distributed in the feature space. A pattern is formed if there are data points sharing certain similar attributes. In geometrical terms it means that these points are close to each other along some spatial dimensions. Classification is possible when the points considered to be in the same class are located in compact (dense) groups within geometrical regions with simple shapes, so that the gaps left between can accommodate a simple decision boundary. Such a geometrical perspective is especially helpful if we consider that most classifiers can also be described by simple geometrical primitives, such as hyperplanes in linear classifiers, Voronoi regions in nearest neighbor classifiers, or piecewise linear surfaces in decision trees.

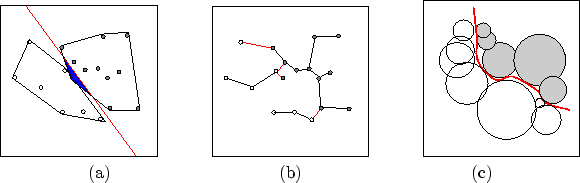
In a recent study (Ho & Basu 2002) with several measures of the geometrical complexity of data sets (Figure 2), we find that a collection of classification problems arising from real-world applications can span a large range in the values of these measures. These problems present different degrees of difficulty to different kinds of classifiers. An analysis of the complexity of the problems for which different classifiers perform the best reveals that classifiers have distinct domains of competence in the space of the complexity measures (Ho 2002, PAA). We expect that more complete and systematic studies of this kind will enable automatic matching of problems to classifiers with good confidence. The complexity measures can also be used to guide the formulation of a classification problem, including definition of the classes, selection of most discriminatory features, and construction of useful feature transformations.

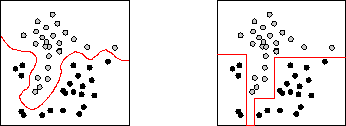
The complexity of a class boundary may interact with other factors that also affect a problem's difficulty. These include the intrinsic ambiguity of classes, due to poor class definitions or poor feature choices (Figure 3), and sample sparsity. Real applications often contain a mixture of these difficulties (Figure 4).

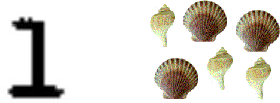When there is a prior expectation that the data may form several coherent groups, clustering methods can help discover such structures. However, many clustering algorithms have strong biases on the types of structures to look for, to the extent that they may coerce the data into undesirable groupings that do not necessarily have clear physical interpretation. One way to guard against such algorithmic artifacts is to first establish the existence of any clustering tendency by statistical testing of a uniformity hypothesis. Similar tests are needed for evidences of more sophisticated structures.

Sometimes the main concern in data analysis is not necessarily to divide the data into disjoint classes, but rather, to explore if there exist any outliers, or whether variations in the data can be described by a trend with a small number of parameters. Methods for estimating the intrinsic dimensionality (Verveer & Duin 1995) attempt to determine how many fundamental parameters there are that determine the variations in the data. This can assist the choice of a low-dimensional smooth surface for modeling the data, and outliers can then be detected by assessing their match to the model. Many of these algorithms have difficulty scaling up to high dimensionality, and they are still under active research.

A challenge ahead is to establish better connections among the various methods for characterizing data geometry, and connections between data geometry and classifier/model geometry. This can help reveal the limitations of the current methods and suggest how they can be overcome. The goal for research in this area is to develop a rich language for geometrical reasoning about point sets in high-dimensional spaces. We expect this to draw input from progresses in differential geometry and its variants incorporating stochastic and discrete processes.

**Figure 2:** Different ways for describing the complexity of a classification boundary: (a) measure of separability of the convex hulls enclosing two classes by a particular linear surface; (b) a count of class-crossing edges in a minimum spanning tree connecting all the points; (c) a count of maximal balls needed to cover all points in each class.
$\begin{figure} \epsscale{0.25} \centering\begin{tabular}{ccc} \plotone{O3-1_f2a.... ...ccc} (a) & \hspace{1.25in} (b) & \hspace{1.25in} (c) \end{tabular}\end{figure}$

**Figure 3:** Class ambiguity due to different reasons. (Left) instrinsic shape ambiguity: lower-case letter ``el'' and numeral ``one'' appear in the same shape in many fonts; the identity can only be determined from context. (Right) non-informative features: there may be sufficient features to classify the shells by shape, but not by the time they were collected or by which hand they were collected. More informative features are needed.
$\begin{figure} \centering\begin{tabular}{cc} \epsscale{0.125} \plotone{O3-1_f3a.... ...\hspace{0.25in} \epsscale{0.25} \plotone{O3-1_f3b.eps} \end{tabular}\end{figure}$

**Figure 4:** Complex class geometry and sparse sample cause ill-defined boundary. More training samples are needed.
$\begin{figure} \centering\begin{tabular}{cc} \epsscale{0.25} \plotone{O3-1_f4a.e... ...epsscale{0.25} \plotone{O3-1_f4b.eps} \vspace{-0.25in} \end{tabular}\end{figure}$

4. Exploratory Visualization of Structures in Data Sets

Given many open challenges in fully automating the pattern discovery process, a strategy with well-proven value is to encourage continuous interaction between domain experts and developers of pattern recognition algorithms.

Domain expertise can bring insights into many stages of solution development. An example is, in classifying galaxies by morphology, how should one apply suitable normalization to the shape measurements to account for variations in the orientation of the rotational axis? Also, for validating discrimination between stars and galaxies, what is the expected luminosity function of each category? In examining patterns in a set of light curves, is the maximum intensity a critical feature to consider? Or should the time series be normalized by the length of each cycle? If a spectral shape can be described by several key parameters, can we see their correlations with other known effects, such as the temperature and kinematic estimates?

A good way to enable the scientists to participate in the process of algorithm development is through the use of an interactive data visualization tool. Ideally, the tool can display data and the results of automatic analysis simultaneously in many different views to support explorations of a wide range of possibilities. This can bring input into many stages of solution development, such as:

Mirage

The Mirage tool (Ho 2003, ADASS) is designed to address these concerns and needs. Mirage is a software experiment on the displays and operations that are most suited to enable pattern discovery from data in multiple types such as numerical vectors, time series, images, and spectra. Many queries about object properties and the relationship between different objects can be translated into geometrical queries on proximity structures in different subspaces (Figure 5), which can be investigated graphically in Mirage. The features we experiment with include the followings.

**Figure 5:** If data projected to two spaces form different cluster structures, questions arise on how the structures correlate with each other. Say, will a walk following a principal curve in one space correspond to a uni-directional walk in another space? Suppose the structure on the left represents groups of objects by color, and the one on the right represents groups by size. We may ask, do objects with the same color always have the same size? When the object sizes increase monotonically, how do their colors change?
$\begin{figure} \centering\begin{tabular}{c} \epsscale{0.5} \plotone{O3-1_f5.eps} \end{tabular}\end{figure}$

**Figure 6:** Screenshots from Mirage: multiple views of the same data set can be opened in an arbitrary layout. Selection from one display can be tracked in other displays. (Left) a table view, two scatter plots, and a time series display in parallel coordinates; (Right) an array of histograms each on a different attribute.
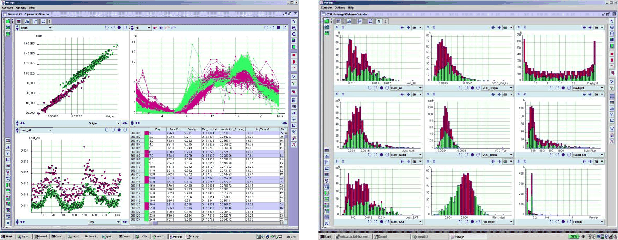$\begin{figure} \epsscale{0.475} \centering\begin{tabular}{cc} \plotone{O3-1_f6a.eps} & \plotone{O3-1_f6b.eps} \end{tabular}\end{figure}$

Simultaneous, multiple views in a flexible layout.

For the primary goal of visualizing data geometry, several types of displays are provided, including basic tools in statistical graphics like histograms, scatter plots, and parallel coordinate plots. The displays are organized as a set of pages; each page can be arbitrarily tiled and any display can go into any tile by drag-and-drop (Figure 6). Displays for special data types, such as images in FITS format, can be plugged in via a standard interface (Carliles et al. 2004).

Core exploration commands and display-specific manipulations.

A set of core commands are implemented by each display module. These are for broadcasting the local selection of a set of data points, highlighting or coloring a broadcast selection, deleting the selection, canceling the highlights or colors, and for switching between monochrome and coloring display modes. In addition, each module can provide local operations suitable for the specific data type, such as manipulation of image color maps, changing resolution of histograms, and zooming in and out of a specific display focus. The selection broadcasting mechanism is very effective for tracking correlations. Items of interest found from one view of the data set can be easily traced in other views. Coordinated sequences of selection and broadcasting can be used to track the effects of systematic changes in data attributes. An example is a step-by-step broadcasting of a standard traversal of a cluster tree, or a walk on each bin of a histogram. When other displays highlight the corresponding data items, one can easily find out if the items are also similar in terms of other attributes.

Facilities for examining tentative modeling.

A tentative classification can be represented as one column in the data matrix, and displayed as one attribute. Selection in that display can be broadcasted to other displays where the effects of the classification can be examined. This way one can easily compare alternative classifications to refine the problem formulation, select features for the classifier, and polish the classifier design. Moreover, data can be imported on the fly by adding columns and rows to the data matrix. Columns added can show newly observed or computed attributes, including classification decisions or predictions from external algorithms. Rows added can be additional samples from the same source, which can be used to check the correctness of a computed model. Continuous adding and removing rows can turn the software into a monitoring tool.

Extensible software design.

The software is designed to be extensible in different ways. Specialized displays can be added as plug-in's. Exploratory actions are organized around a small command interpreter, which can be activated via an application interface. In addition, the software has a slot for plugging in an ``Action'' panel, which can be used to encapsulate data updating and analysis operations useful for the current task. The Mirage window can also be embedded into and invoked by wrapper programs which can implement more sophisticated data access methods (Carliles et al. 2004).

Scripting for repeatable, cooperative investigation.

Data analysis is seldom an individual effort. To enable easy repetition and sharing of exploration commands and results in a research team, Mirage provides text-driven commands and scripting facilities. Scripts can be passed around for replay. They can also be systematically constructed by simple programs to make animations.

Early applications of Mirage confirmed the effectiveness of many of these designs, and suggested improvements in several ways. Programmable display layouts, software state saving and restoration, and automated explorations are among the most desired. We are also investigating better ways to cooperate with external analysis code while maintaining a simple and modular core architecture.

5. Conclusions

Research in automatic pattern recognition has resulted in the identification of several key tasks and the development of a large collection of methods. Yet we are still missing systematic procedures for matching methods to problems, largely because of a lack of effective ways for characterizing data complexity. Early investigations reveal the multi-facet nature of data complexity and its relationship to classifier performance. A better understanding of the data geometry in high-dimensional spaces is needed.

Convenient visualization tools can provide better insight into the data geometry, and to provide domain experts easy access to the analysis process. They can closely monitor each stage of solution development, and offer frequent feedback in key steps like feature selection, evaluation of tentative classifications, and validation of final results. The Mirage software is designed to enable such exchanges. It is constructed as an extensible platform for supporting knowledge discovery in various degrees of automation. We are in continuous experimentation on ways to improve it towards a rich tool for interactive pattern recognition.

Acknowledgments

I thank E.B. Mansilla for the classifier examples in Figure 1, and many early users of Mirage for their encouragement and suggestions.

References

Ho, T.K., Basu, M. 2002, IEEE Trans. on Pattern Analysis & Machine Intelligence, 24, 3, 289-300.

Jain, A.K., Duin, R.P.W., Mao, J. 2000, IEEE Trans. on Pattern Analysis & Machine Intelligence, 22, 1, 4-37.

Trahanias, P., Skordalakis E. 1990, IEEE Trans. on Pattern Analysis & Machine Intelligence, 12, 7, 648-657.

Verveer, P.J., Duin, R.P.W. 1995, IEEE Trans. on Pattern Analysis & Machine Intelligence, 17, 1, 81-86.

Promises and Challenges in Automatic Pattern Recognition

Abstract:

1. Introduction