Superresolution is a useful technique in a variety of applications (Schultz & Stevenson, 1996; Hardie, Barnard, & Armstrong, 1997), and recently, researchers have begun to investigate the use of wavelets for superresolution image reconstruction (Nguyen, Milanfar, & Golub, 2001). We present a new method for superresolution image reconstruction based on the wavelet transform in the presence of Gaussian noise and on an analogous multiscale approach in the presence of Poisson noise. To construct the superresolution image, we use an approach based on maximum penalized likelihood estimation. The reconstructed image is the argument (in our case the superresolution image) that maximizes the sum of a log-likelihood function and a penalizing function. The penalizing function can be specified by an ad hoc smoothness measure, a Bayesian prior distribution for the image (Hebert & Leahy, 1989; Green, 1990), or a complexity measure (Liu & Moulin, 2001). Smoothness measures include simple quadratic functions that measure the similarity between the intensity values of neighboring pixels, as well as non-quadratic measures that better preserve edges. Similar penalty functions result from Markov Random Field (MRF) priors. Complexity measures are usually associated with an expansion of the intensity image with respect to a set of basis functions (e.g. Fourier or wavelet) and count the number of terms retained in a truncated or pruned series (Saito, 1994; Krim & Schick, 1999); the more terms (basis functions) used to represent the image, the higher the complexity measure. Many algorithms (e.g. Expectation-Maximization algorithms, the Richardson Lucy algorithm, or close relatives) have been developed to compute MPLEs under various observation models and penalization schemes.
Wavelets and multiresolution analysis are especially well-suited for astronomical image processing because they are adept at providing accurate, sparse representations of images consisting of smooth regions with isolated abrupt changes or singularities ( e.g. stars against a dark sky). Many investigators have considered the use of wavelet representations for image denoising, deblurring, and image reconstruction; for examples, see Mallat, 1998, and Starck, Murtagh, & Bijaoui, 1998. The proposed approach uses an EM algorithm for superresolution image reconstruction based on a penalized likelihood formulated in the wavelet domain. Regularization is achieved by promoting a reconstruction with low-complexity, expressed in terms of the wavelet coefficients, taking advantage of the well known sparsity of wavelet representations.
The EM algorithm proposed here extends the work of Nowak & Kolaczyk, 2000, and
Figueiredo & Nowak, 2002, which addressed image deconvolution with a method
that combines the efficient image representation offered by the discrete wavelet
transform (DWT) with the diagonalization of the convolution operator obtained in
the Fourier domain. The algorithm alternates between an E-step
based on the fast Fourier transform (FFT) and a DWT-based M-step, resulting in
an efficient iterative process requiring ![]() operations per iteration,
where
operations per iteration,
where ![]() is the number of pixels in the superresolution image.
is the number of pixels in the superresolution image.
From the formulation above, it is clear that superresolution image
reconstruction is a type of inverse problem in which the operator to be
inverted, ![]() , is partially unknown due to the unknown shifts and rotations of
the observations. The first step of our approach is to estimate these parameters
by registering the low-resolution observations to one another. Using these
estimates, we reconstruct an initial superresolution image estimate
, is partially unknown due to the unknown shifts and rotations of
the observations. The first step of our approach is to estimate these parameters
by registering the low-resolution observations to one another. Using these
estimates, we reconstruct an initial superresolution image estimate
![]() . This
estimate is used in the third step, where we re-estimate the shift and rotation
parameters by registering each of the low resolution observations to the initial
superresolution estimate. Finally, we use a wavelet-based EM algorithm to solve
for
. This
estimate is used in the third step, where we re-estimate the shift and rotation
parameters by registering each of the low resolution observations to the initial
superresolution estimate. Finally, we use a wavelet-based EM algorithm to solve
for
![]() using the registration parameter estimates. We begin by describing a
wavelet-based method for the Gaussian noise model, and follow that by a
discussion of a multiscale technique for Poisson data. Each of these steps is
detailed below.
using the registration parameter estimates. We begin by describing a
wavelet-based method for the Gaussian noise model, and follow that by a
discussion of a multiscale technique for Poisson data. Each of these steps is
detailed below.
The first step in the proposed method is to register the observed low-resolution
images to one another using a Taylor series expansion. This was proposed by
Irani and Peleg, 1991. In particular, let ![]() and
and ![]() be the continuous
images underlying the sampled images
be the continuous
images underlying the sampled images ![]() and
and ![]() , respectively. If
, respectively. If
![]() is equal to a shifted, rotated version of
is equal to a shifted, rotated version of ![]() , then we have the
relation
, then we have the
relation
|
After the registration parameters have been initially estimated using the above
method, we use these estimates to calculate an initial superresolution image as
described in Section 4.. This initial image estimate is then used to
refine the registration parameter estimates. The method is the same as above,
but instead of registering a low resolution estimate, ![]() , to another low
resolution estimate,
, to another low
resolution estimate, ![]() , we instead register it to
, we instead register it to
![]() . The
results of this refinement are displayed in gray in Figure
1. From these plots, it is clear that the Taylor series
based approach can produce highly accurate results. However, in low SNR
scenarios, where confidence in registration parameter estimates may be low, the
estimates can be further refined at each iteration of the proposed EM algorithm,
as discussed in the following sections.
. The
results of this refinement are displayed in gray in Figure
1. From these plots, it is clear that the Taylor series
based approach can produce highly accurate results. However, in low SNR
scenarios, where confidence in registration parameter estimates may be low, the
estimates can be further refined at each iteration of the proposed EM algorithm,
as discussed in the following sections.
Note that the motion model considered here encompasses only shift and rotation movement. When recording still or relatively still objects distant from the imaging device, this model is sufficient. More sophisticated models are an area of open research.
The Gaussian observation model in (1) can be written with respect
to the DWT coefficients
![]() , where
, where
![]() and
and ![]() denotes the
inverse DWT operator (Mallat, 1998):
denotes the
inverse DWT operator (Mallat, 1998):
An analogous formulation is possible for the Poisson noise model. In this case,
photon projections can be described statistically as follows. Photons are
emitted (from the emission space) according to a high resolution intensity
![]() . Those photons emitted from location
. Those photons emitted from location ![]() are detected (in the detection
space) at position
are detected (in the detection
space) at position ![]() with transition probability
with transition probability ![]() , where
, where ![]() is the
superresolution operator from (2). In such cases, the measured
data are distributed according to
is the
superresolution operator from (2). In such cases, the measured
data are distributed according to
From these formulations of the problem for Gaussian and Poisson data, the EM
algorithm produces a sequence of estimates
![]() by alternately applying two steps:
by alternately applying two steps:
In the Poisson case, this step is reduced to
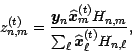
In the Poisson case, the M-Step is equivalent to photon-limited image denoising. In practice, this commonly consists of performing maximum likelihood estimation, but these estimates are known to diverge from the true image after several iterations. The denoising can also be accomplished using the Haar-based maximum penalized likelihood estimation method we developed in Willett & Nowak, 2003; the MPLE function employed here is
where
![]() is the Poisson likelihood of observing photon counts
is the Poisson likelihood of observing photon counts
![]() given intensities
given intensities
![]() and
and
![]() is the number of non-zero coefficients in
the Haar-based multiscale representation of
is the number of non-zero coefficients in
the Haar-based multiscale representation of
![]() and
and ![]() is
the total number of photons in the observation vector
is
the total number of photons in the observation vector
![]() . In maximizing this
function, the resulting reconstruction will be one that has a relatively high
likelihood value as well as a relatively low complexity Haar representation.
This denoising procedure is a bottom-up tree pruning algorithm which requires
. In maximizing this
function, the resulting reconstruction will be one that has a relatively high
likelihood value as well as a relatively low complexity Haar representation.
This denoising procedure is a bottom-up tree pruning algorithm which requires
![]() operations.
operations.
In both the Gaussian and Poisson noise cases, the proposed method has the advantage that the M-step is a denoising procedure, and the multiscale methods employed here are both near-minimax optimal.
In low SNR cases, where confidence in the initial estimates of the shift and
rotation parameters may be low, the proposed algorithm can be modified by simply
inserting an additional step in which the parameter estimates are updated based
on the current estimate of the superresolution image
![]() , as
described in the previous section. Similarly, if the blurring operator is only
partially known, its parameters can also be updated at each iteration of the
proposed algorithm. The resulting scheme is not a standard EM algorithm, but it
is guaranteed not to decrease the penalized likelihood function.
, as
described in the previous section. Similarly, if the blurring operator is only
partially known, its parameters can also be updated at each iteration of the
proposed algorithm. The resulting scheme is not a standard EM algorithm, but it
is guaranteed not to decrease the penalized likelihood function.
We reconstructed two superresolution images to demonstrate the practical
effectiveness of the proposed algorithms. A sample low-resolution satellite
image of earth is displayed in Figure 2(a). Sixteen such
![]() images were generated using an original
images were generated using an original
![]() image
(Figure 2(c), with values ranging from 0 to 255), which was
shifted and rotated by a random, subpixel amount, distorted by a
image
(Figure 2(c), with values ranging from 0 to 255), which was
shifted and rotated by a random, subpixel amount, distorted by a ![]() uniform blur, and contaminated with additive white Gaussian noise with variance
uniform blur, and contaminated with additive white Gaussian noise with variance
![]() . The superresolution image in Figure
2(b) was reconstructed using the wavelet-based EM algorithm
described above for
. The superresolution image in Figure
2(b) was reconstructed using the wavelet-based EM algorithm
described above for
![]() . In the simulation, the
estimate is initialized with a least-squares superresolution estimate of
relatively poor quality. While not presented here, experiments have shown that
the proposed approach is competitive with the state of the art in
superresolution image reconstruction.
. In the simulation, the
estimate is initialized with a least-squares superresolution estimate of
relatively poor quality. While not presented here, experiments have shown that
the proposed approach is competitive with the state of the art in
superresolution image reconstruction.
| ||||||||
In our second simulation, we studied the effect of the proposed method on an
image of stars. The original image is displayed in Figure
3(c). The data for this simulation was generated using the
same procedure as for the Earth image. Note from the sample observation image in
Figure 3(a) that several stars are indistinguishable prior
to superresolution image reconstruction, but that after the application of the
proposed method these stars are clearly visible in Figure
3(b). The superresolution image in Figure
3(d) was generated using the same procedure but with only
two observation images. Clearly the quality of this result is less than the
quality achievable with more observations, but significantly more stars are
distinguishable in the output than in any one of the observations. This implies
that the proposed method may be useful even for small sets of observations.
Finally, Figure 3(e) displayed the output of our multiscale
method for Poisson noise. In the case, the mean photon count was ![]() . As in
the Gaussian case, the improvement in resolution is significant.
. As in
the Gaussian case, the improvement in resolution is significant.
| ||||||||||||
In this paper we present a multiscale approach for superresolution image reconstruction in the presence of either Gaussian or Poisson noise. This approach uses several shifted, rotated, blurred, noisy observations to construct a new image with higher resolution than any of the observations. Because of the multiscale complexity regularization used in the the EM reconstruction algorithm, our approach is robust to noise. This is demonstrated for several practical examples. Notably, we demonstrated that stars which are irresolvable in any individual observation can be clearly distinguished after superresolution image reconstruction, even when using only two observation images.
Future work includes speeding the convergence of the proposed method using a new technique described in (Salakhutdinov & Roweis, 2003) and a more Bayesian approach in which the shift and rotation parameters are integrated out of the problem formulation. In addition, there are several questions still to be addressed, including: How does the blur radius impact reconstruction quality? How much can resolution be recovered at what accuracy? How can the proposed multiscale methods be extended to optimally process data collected by photon detector cells with spatially varying sensitivities? Despite these open areas of research, however, we feel that wavelet-based superresolution has the potential to make a significant impact on astronomical imaging.
Donoho, D., 1999, Ann. Statist., 27, 859
Figueiredo, M. & Nowak, R., 2002, IEEE Transactions on Image Processing, 29, 1033
Figueiredo, M. & Nowak, R., 2001, IEEE Transactions on Image Processing, 10, 1322
Green, P. J., 1990, IEEE Trans. Med. Imaging, 9, 84
Hardie, R. C., Barnard, K. J., & Armstrong, E. E., 1997, IEEE Transactions on Image Processing, 6, 1621
Hebert, T. & Leahy, R., 1989, IEEE Trans. Med. Imaging, 8, 194
Irani, M. & Peleg, S. 1991, Computer Vis. Graph. Image Process.: Graph. Models Image Process, 53, 231
Kolaczyk, E., 1999, J. Amer. Statist. Assoc., 94, 920
Kolaczyk, E. & Nowak, R., 2003,
to appear in the Annals of Statistics, ``Multiscale Likelihood Analysis and Complexity Penalized Estimation'',
http://www.ece.wisc.edu/~nowak/pubs.html
Krim, H., & Schick, I. C., 1999, IEEE Trans. on Information Theory, 45
Landweber, L., 1951, American Journal of Mathematics, 73, 615
Liu, J. & Moulin, P., 2001, IEEE Transactions on Image Processing, 10, 841
Mallat, S., 1998, A Wavelet Tour of Signal Processing
Nowak, R., & Kolaczyk, E., 2000, IEEE Transactions on Information Theory, 46, 1811
Nguyen, N., Milanfar, P., & Golub, G., 2001, IEEE Transactions on Image Processing, 10, 573
Saito, N, 1994, Wavelets in Geophysics, ed. Foufoula-Georgiou and Kumar
Salakhutdinov, R. & Roweis, S., 2003, International Conference on Machine Learning, 664
Schultz, R. R. & Stevenson, R. L., 1996, IEEE Transactions on Image Processing, 5, 996
Starck, J., Murtagh, F., & Bijaoui, A., 1998, Image Processing and Data Analysis: The Multiscale Approach
Timmermann, K. & Nowak, R, 1999, IEEE Transactions on Information Theory, 45, 846
Willett, R. & Nowak, R., 2003, IEEE Transactions of Medical Imaging, 22, 332