Next: PacketLib: A C++ Library for Scientific Satellite Telemetry Applications
Up: Data Analysis Software and Systems
Previous: XAssist: A System for the Automation of X-ray Astrophysics Analysis
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
Bhatnagar, S., Urvashi, R. V., & Nityananda, R. 2003, in ASP Conf. Ser., Vol. 295 Astronomical Data Analysis Software and Systems XII, eds. H. E. Payne, R. I. Jedrzejewski, & R. N.
Hook (San Francisco: ASP), 469
Solving for Polarization Leakage in Radio Interferometers Using
Unpolarized Source
S. Bhatnagar,1 R. V. Urvashi2
and R. Nityananda3
National Center for Radio Astrophysics (NCRA), Pune, India 411007
Abstract:
This paper presents an algorithm for solving antenna based
polarization leakage in a radio interferometer using co-polar
observations of unpolarized sources. If ignored, polarization leakage
manifests itself as closure errors in parallel hand (co-polar)
visibilities. Many working radio telescopes offer observational
advantages for observations in non-polar mode (e.g., higher frequency
resolution, lower integration time, etc.). Many observations are
therefore done in non-polar mode and the computation of antenna based
leakage gains in co-polar visibilities is scientifically useful for
debugging and calibrating the instrument. Also, this is a useful
option to use when one cannot or does not want to put in the
additional measurement effort to determine the leakage term by means
of cross-polar measurements. We also present results from test data
taken with the Giant Meterwave Radio Telescope (GMRT) and discuss the
degeneracy in the solutions and the equivalence of the leakage induced
closure phase and the Pancharatnam phase of optics.
Co-polar output of an interferometer, can be written as
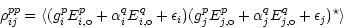 |
(1) |
where 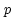 and
and 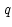 are two orthogonal polarization states
(R and L or X and Y),
are two orthogonal polarization states
(R and L or X and Y), 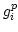 the antenna complex gain for the
the antenna complex gain for the 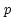 -channel of antenna
-channel of antenna 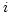 ,
, 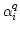 the leakage of q-signal
into the p-channel,
the leakage of q-signal
into the p-channel, 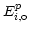 the ideal response of
the p-channel to the incident radiation, and
the ideal response of
the p-channel to the incident radiation, and 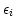 the
antenna based additive noise. For an unpolarized point source,
the
antenna based additive noise. For an unpolarized point source,
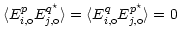 and
and
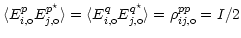 where
where 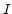 is the total intensity. Writing
is the total intensity. Writing
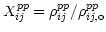 we get
we get
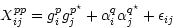 |
(2) |
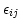 is the independent baseline based noise. Usually this
represents the noise in
is the independent baseline based noise. Usually this
represents the noise in
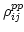 after the correlation
operation plus the antenna based noise.
after the correlation
operation plus the antenna based noise. 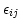 therefore is
a measure of the true closure errors in the system and is
usually small. Assuming
therefore is
a measure of the true closure errors in the system and is
usually small. Assuming 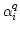 s to be negligible, the usual
Selfcal algorithm estimates
s to be negligible, the usual
Selfcal algorithm estimates 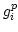 s such that
s such that
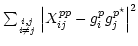 is minimized.
However, leakage due to mechanical and/or electronic imperfections in
the feed, cross talk, squint of cross-polar primary beam,
off-axis primary beam polarization, etc., is hard to eliminate making
is minimized.
However, leakage due to mechanical and/or electronic imperfections in
the feed, cross talk, squint of cross-polar primary beam,
off-axis primary beam polarization, etc., is hard to eliminate making
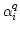 s potentially non-negligible.
s potentially non-negligible.
In the presence of significant 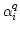 s (compared to
s (compared to
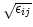 ), ignoring the second term in Equation 2
will be equivalent to a system with apparent increased closure
noise (
), ignoring the second term in Equation 2
will be equivalent to a system with apparent increased closure
noise (
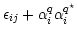 instead of just
instead of just
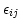 ). Hence, polarization leakage manifests as
increased closure errors. This has also been pointed out by Rogers
(1983) in the context of VLBA observations, and extensive study by
Massi & Aaron (1997) for EVN shows that imaging quality is limited by
these errors.
). Hence, polarization leakage manifests as
increased closure errors. This has also been pointed out by Rogers
(1983) in the context of VLBA observations, and extensive study by
Massi & Aaron (1997) for EVN shows that imaging quality is limited by
these errors.
When solving for only 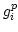 using co-polar visibilities, the
using co-polar visibilities, the
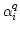 s appear as increased closure noise and will result in
non-optimal solutions. Hence, a simultaneous solution for
s appear as increased closure noise and will result in
non-optimal solutions. Hence, a simultaneous solution for 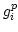 and
and
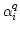 would be optimal. In the presence of significant
polarization leakage, the correct estimator for the true closure
noise is given by
would be optimal. In the presence of significant
polarization leakage, the correct estimator for the true closure
noise is given by
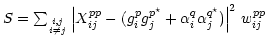 where
where 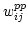 are the weights. Equating
the partial derivatives
are the weights. Equating
the partial derivatives
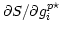 ,
,
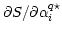 to zero, we get a set of
non-linear equations for
to zero, we get a set of
non-linear equations for 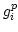 s and
s and 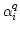 s which can be
iteratively solved (Bhatnagar & Nityananda 2001).
s which can be
iteratively solved (Bhatnagar & Nityananda 2001).
3. Solution Degeneracy, Simulations and the GMRT Experiment
Simulations demonstrate that with the use of the above algorithm, the
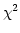 remains constant with increasing leakage, and that it solves
for
remains constant with increasing leakage, and that it solves
for 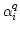 s only if they are significant (i.e., distinguishable
from
s only if they are significant (i.e., distinguishable
from
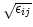 , Bhatnagar & Nityananda 2001). The
decrease in
, Bhatnagar & Nityananda 2001). The
decrease in 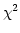 , compared to that given by Selfcal, is due to the
use of the correct estimator for the closure noise and not because of
extra free parameters (the
, compared to that given by Selfcal, is due to the
use of the correct estimator for the closure noise and not because of
extra free parameters (the 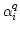 s) in the problem. The
solutions for
s) in the problem. The
solutions for 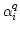 s are therefore physically meaningful.
s are therefore physically meaningful.
However, an obvious degeneracy is rotation of all the 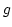 's by a
common phase factor and the
's by a
common phase factor and the 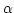 s by an, in general different,
phase factor,
does not affect the left hand side of Equation 2. We also have
the freedom to choose a suitable basis in polarization space (see
Bhatnagar & Nityananda 2001 for details). We choose this
basis in such a way that the sum of the absolute squares of all the
leakage terms is minimized.
Carrying out the maximization of
s by an, in general different,
phase factor,
does not affect the left hand side of Equation 2. We also have
the freedom to choose a suitable basis in polarization space (see
Bhatnagar & Nityananda 2001 for details). We choose this
basis in such a way that the sum of the absolute squares of all the
leakage terms is minimized.
Carrying out the maximization of
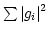 by the
method of Lagrange multipliers, subject to a constant
by the
method of Lagrange multipliers, subject to a constant 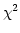 , we
obtain the condition that
, we
obtain the condition that
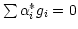 (implying that the
leakage coefficients be orthogonal to the gains) and can be
incorporated by first choosing an overall phase for the
(implying that the
leakage coefficients be orthogonal to the gains) and can be
incorporated by first choosing an overall phase for the 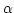 's so
that
's so
that
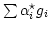 is real. Then, carry out a rotation in
the
is real. Then, carry out a rotation in
the 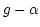 plane by an angle
plane by an angle 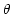 satisfying
satisfying
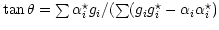 . Results of such a transform on simulated
data are shown in Figure 1. The absolute frame of
reference in which
. Results of such a transform on simulated
data are shown in Figure 1. The absolute frame of
reference in which 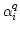 s are measured, also remain
undetermined since the source is unpolarized. However this degeneracy
is same as that in the phase of
s are measured, also remain
undetermined since the source is unpolarized. However this degeneracy
is same as that in the phase of 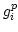 s and is not important for
correcting the data.
s and is not important for
correcting the data.
Figure:
Simulations showing the decoupling of the solutions
for 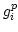 s and
s and 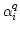 s. Squares are the input test
s. Squares are the input test 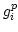 s and
s and
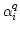 s on the complex plane while diamonds are the
solutions. The arrows show the length and direction of correction due to the
transformation.
s on the complex plane while diamonds are the
solutions. The arrows show the length and direction of correction due to the
transformation.
 |
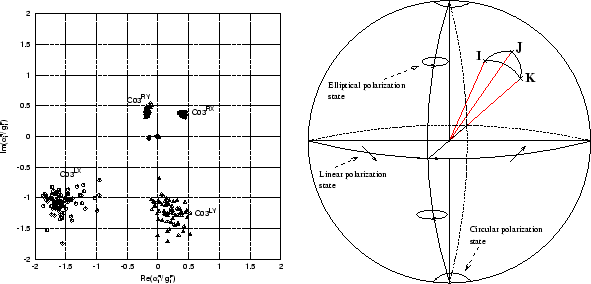
We used GMRT L-band test data with circularly polarized feed on
only one antenna ( C03 in Figure 2) and linear
feeds on the rest. In the mean linear basis of all the antennas,
C03 appears as an antenna with
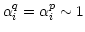 (
(
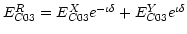 ; ideally
; ideally 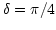 ). The
fractional leakage (
). The
fractional leakage (
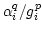 ) for all antennas is plotted in
the complex plane in Figure 2[Left]. Mean leakage of all
the antennas define the reference frame in which the leakage of
the nominally linear antennas is minimum. All but one nominally
linearly polarized antennas are at the origin (minimal leakage);
points corresponding to C03 are farthest from the center,
grouped
) for all antennas is plotted in
the complex plane in Figure 2[Left]. Mean leakage of all
the antennas define the reference frame in which the leakage of
the nominally linear antennas is minimum. All but one nominally
linearly polarized antennas are at the origin (minimal leakage);
points corresponding to C03 are farthest from the center,
grouped
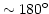 apart.
apart.
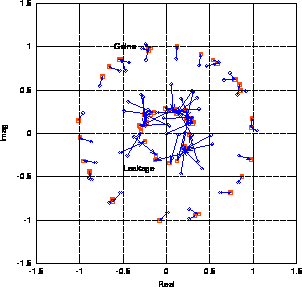
Figure:
[Left] Plot of
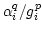 for all GMRT
antennas.
for all GMRT
antennas. 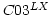 and
and 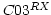 (open
circles) are from correlations of R- and L-channel of C03 with
X-channel of other linear antennas. Similarly for
(open
circles) are from correlations of R- and L-channel of C03 with
X-channel of other linear antennas. Similarly for 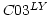 and
and
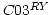 (triangles). One of the linearly
polarized antennas is leakier than the others and L-channel of C03 is
noisier than its R-channel. [Right] Poincaré sphere
representation of polarization states.
Closure phase between three coherent but non-identical antennas
represented by the points I,J and K is equal to half the solid angle
of IJK.
(triangles). One of the linearly
polarized antennas is leakier than the others and L-channel of C03 is
noisier than its R-channel. [Right] Poincaré sphere
representation of polarization states.
Closure phase between three coherent but non-identical antennas
represented by the points I,J and K is equal to half the solid angle
of IJK.
 |
A general elliptically polarized state can be written as a
superposition of two states represented by the vector
![$[\cos
\theta/2~~\sin \theta/2e^{\iota\phi}]$](img44.gif) in the basis defined by the left- and
right-circular polarization states. Clearly,
in the basis defined by the left- and
right-circular polarization states. Clearly,
 corresponds to linear polarization and
corresponds to linear polarization and
 to
elliptical polarization. The Poincaré sphere representation of the
state of polarization maps the general elliptic state to the point
(
to
elliptical polarization. The Poincaré sphere representation of the
state of polarization maps the general elliptic state to the point
( ) on the sphere. It can be shown that the closure
phase between three coherent, non-identical, antennas (points
) on the sphere. It can be shown that the closure
phase between three coherent, non-identical, antennas (points  ,
,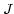 and
and 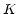 in Figure 2[Right]) is equal to half the solid
angle
in Figure 2[Right]) is equal to half the solid
angle 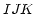 . This goes by the name
Pancharatnam/Geometric/Berry's phase in optical literature
(Pancharatnam, 1956). The closure phase due to polarization
mis-matches between phased antennas in a radio interferometer
therefore naturally measures the Pancharatnam phase.
The method described here measures the polarization leakage
using the co-polar visibilities for an unpolarized calibrator.
It is a useful tool for studying the polarization purity of the
antennas of radio interferometers. Simultaneous solution of gain and
leakage ensures that the method factorizes for leakage only if they
are distinguishable from intrinsic true closure noise. The
degeneracy between solutions of antenna based complex gains and
leakage is broken by physically meaningful transform and the solutions
can be used to remove leakage induced closure errors. Geometric
interpretation of the results on the Poincaré sphere shows that the
leakage induced closure phase is same as the Pancharatnam phase and
the degeneracy in the solutions can be understood as a rigid rotation
of the Poincaré sphere.
. This goes by the name
Pancharatnam/Geometric/Berry's phase in optical literature
(Pancharatnam, 1956). The closure phase due to polarization
mis-matches between phased antennas in a radio interferometer
therefore naturally measures the Pancharatnam phase.
The method described here measures the polarization leakage
using the co-polar visibilities for an unpolarized calibrator.
It is a useful tool for studying the polarization purity of the
antennas of radio interferometers. Simultaneous solution of gain and
leakage ensures that the method factorizes for leakage only if they
are distinguishable from intrinsic true closure noise. The
degeneracy between solutions of antenna based complex gains and
leakage is broken by physically meaningful transform and the solutions
can be used to remove leakage induced closure errors. Geometric
interpretation of the results on the Poincaré sphere shows that the
leakage induced closure phase is same as the Pancharatnam phase and
the degeneracy in the solutions can be understood as a rigid rotation
of the Poincaré sphere.
Acknowledgments
We thank the GMRT staff, NCRA, BITS and NRAO for their support and co-operation.
References
Bhatnagar, S. & Nityananda, R. 2001, A&A, 375, 344-350
Massi, M. & Aaron, S. 1997, EVN Tech. Memo, N75
Pancharatnam, S. 1956, S. Proc. Indian Aad. Sci., A44, 247
Rogers, A. E. E. 1983, VLB Array Memo No. 253
Footnotes
- ... Bhatnagar,1
- Now at the National Radio Astronomy Observatory (NRAO), Socorro, NM 87801, Email: sbhatnag@aoc.nrao.edu
- ... Urvashi2
- Birla Institute of Technology & Science (BITS), Pilani, India and
now the department of Computer Science and Engineering, UCSD, CA
92093. Email: uraovenk@cs.ucsd.edu
- ... Nityananda3
- Email: rajaram@ncra.tifr.res.in
© Copyright 2003 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: PacketLib: A C++ Library for Scientific Satellite Telemetry Applications
Up: Data Analysis Software and Systems
Previous: XAssist: A System for the Automation of X-ray Astrophysics Analysis
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
![]() s (compared to
s (compared to
![]() ), ignoring the second term in Equation 2
will be equivalent to a system with apparent increased closure
noise (
), ignoring the second term in Equation 2
will be equivalent to a system with apparent increased closure
noise (
![]() instead of just
instead of just
![]() ). Hence, polarization leakage manifests as
increased closure errors. This has also been pointed out by Rogers
(1983) in the context of VLBA observations, and extensive study by
Massi & Aaron (1997) for EVN shows that imaging quality is limited by
these errors.
). Hence, polarization leakage manifests as
increased closure errors. This has also been pointed out by Rogers
(1983) in the context of VLBA observations, and extensive study by
Massi & Aaron (1997) for EVN shows that imaging quality is limited by
these errors.
![]() 's by a
common phase factor and the
's by a
common phase factor and the ![]() s by an, in general different,
phase factor,
does not affect the left hand side of Equation 2. We also have
the freedom to choose a suitable basis in polarization space (see
Bhatnagar & Nityananda 2001 for details). We choose this
basis in such a way that the sum of the absolute squares of all the
leakage terms is minimized.
Carrying out the maximization of
s by an, in general different,
phase factor,
does not affect the left hand side of Equation 2. We also have
the freedom to choose a suitable basis in polarization space (see
Bhatnagar & Nityananda 2001 for details). We choose this
basis in such a way that the sum of the absolute squares of all the
leakage terms is minimized.
Carrying out the maximization of
![]() by the
method of Lagrange multipliers, subject to a constant
by the
method of Lagrange multipliers, subject to a constant ![]() , we
obtain the condition that
, we
obtain the condition that
![]() (implying that the
leakage coefficients be orthogonal to the gains) and can be
incorporated by first choosing an overall phase for the
(implying that the
leakage coefficients be orthogonal to the gains) and can be
incorporated by first choosing an overall phase for the ![]() 's so
that
's so
that
![]() is real. Then, carry out a rotation in
the
is real. Then, carry out a rotation in
the ![]() plane by an angle
plane by an angle ![]() satisfying
satisfying
![]() . Results of such a transform on simulated
data are shown in Figure 1. The absolute frame of
reference in which
. Results of such a transform on simulated
data are shown in Figure 1. The absolute frame of
reference in which ![]() s are measured, also remain
undetermined since the source is unpolarized. However this degeneracy
is same as that in the phase of
s are measured, also remain
undetermined since the source is unpolarized. However this degeneracy
is same as that in the phase of ![]() s and is not important for
correcting the data.
s and is not important for
correcting the data.

