A filter has been designed to reduce these effects and it has been inserted in the feedback loop of the telescope mount servo. Engineering tests and observers reports have noted a marked improvement in the telescope's tracking performance.
A filter has been designed to reduce these effects and it has been inserted in the feedback loop of the telescope mount servo. Engineering tests and observers reports have noted a marked improvement in the telescope's tracking performance.
UKIRT uses high resolution (24 bit) absolute shaft encoders to determine the telescope's orientation. These have been long known to have two systematic errors:
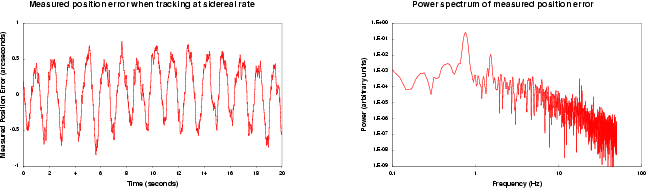
This error is shown by the two plots in Figure 1. The first is the measured position error when tracking at sidereal rates and it clearly shows the dominant sinusoidal error. The second is the power spectrum of the motion, which confirms the peak is at 0.76 Hz. There are a number of interesting aspects to the motion:
Fortunately, the error is not seen whilst auto-guiding since the telescope servo uses the guide signals directly, thus bypassing the encoders. However, since UKIRT is an infra-red telescope it does observe fields where there are no visible guide stars since the visible light is heavily obscured by dust. At these times auto-guiding is not available and so the tracking performance is paramount.
 |
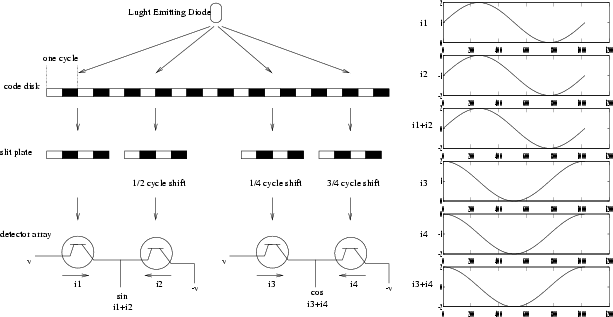
To understand the errors we must look at how the encoder produces a
resolution of ![]() bits using a code disk with only
bits using a code disk with only ![]() rulings. This is illustrated in Figure 2. Light
from an LED illuminates a code disc and slit plate, both of which have
similar rulings but move relative to each other as the axis
rotates. Light that passes through the code disk and slit plate is
detected by photosensitive diodes. The slit plates are arranged in
groups of four, with a
rulings. This is illustrated in Figure 2. Light
from an LED illuminates a code disc and slit plate, both of which have
similar rulings but move relative to each other as the axis
rotates. Light that passes through the code disk and slit plate is
detected by photosensitive diodes. The slit plates are arranged in
groups of four, with a ![]() period offset between each member
of the group. The signals from the four detectors provide sine and
cosine signals and they are combined using an arc-tangent
multiplier. The result is digitized to give the additional 8 bits of
resolution.
period offset between each member
of the group. The signals from the four detectors provide sine and
cosine signals and they are combined using an arc-tangent
multiplier. The result is digitized to give the additional 8 bits of
resolution.
 |
Minor imperfections in the encoder generate systematic errors in the measurement. For example, an error in the positioning of the slit plate will result in an approximately sinusoidal error with a period equal to the period of the code disk. These imperfections are the source of the periodic errors we observe.
In modeling the system we assume the measured position at sampling
time ![]() , say
, say ![]() , can be represented by three terms, e.g.:
, can be represented by three terms, e.g.:
where ![]() is the true telescope position,
is the true telescope position, ![]() is the
systematic periodic measurement error and
is the
systematic periodic measurement error and ![]() is a random measurement
error, which includes the quantization error.
is a random measurement
error, which includes the quantization error.
To estimate the measurement errors we introduce a periodic filter to
model ![]() and a Kalman filter to model
and a Kalman filter to model ![]() . The error estimates are
then subtracted from the encoder reading in the encoder feedback path.
. The error estimates are
then subtracted from the encoder reading in the encoder feedback path.
The periodic filter assumes the periodic errors are of the form:
where ![]() ,
, ![]() ,
, ![]() and
and ![]() are determined by
experiment. For the UKIRT hour angle encoder,
are determined by
experiment. For the UKIRT hour angle encoder, ![]() and
and ![]() are
are ![]() and
and ![]() arcseconds respectively, whilst
arcseconds respectively, whilst ![]() and
and ![]() are
are
![]() and
and ![]() radians. We have found these numbers to be remarkably
stable which implies that the errors probably derive from a constant
misalignment of the encoder slit plates.
radians. We have found these numbers to be remarkably
stable which implies that the errors probably derive from a constant
misalignment of the encoder slit plates.
The Kalman filter design is based on the assumption that ![]() is
truly random with a Gaussian form and a standard deviation comparable to
the size of the least significant bit of the encoder. This filter is
primarily intended to reduce the quantization errors, but an unexpected
side effect was that it significantly improved the performance of the
periodic filter. The conclusion we drew was that the errors remaining
after the periodic filter were fairly Gaussian and noise like and so
were correctly rejected by the Kalman filter.
is
truly random with a Gaussian form and a standard deviation comparable to
the size of the least significant bit of the encoder. This filter is
primarily intended to reduce the quantization errors, but an unexpected
side effect was that it significantly improved the performance of the
periodic filter. The conclusion we drew was that the errors remaining
after the periodic filter were fairly Gaussian and noise like and so
were correctly rejected by the Kalman filter.
The final advantage of the filter is that it enabled us to increase the loop gain of the system by a factor of 2, thereby improving the frequency response in the presence of other disturbances.
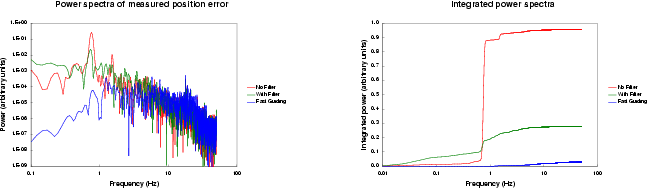
Since the encoder is the source of the errors, it cannot be used to determine the quality of the end result. Instead, we used position measurements made at 100 Hz on a bright star. We have done this in three modes:
The results are presented in Figure 3. The left
figure is the traditional power spectra, and the right figure plots the
total power integrated up to a particular frequency. Note that, whilst
the fast guider gives clearly the best results, the effect of the
periodic encoder error has been dramatically reduced when tracking. This
is seen best in integrated power diagram since the power is on a linear,
rather than a logarithmic, scale. The total power (i.e. the variance) of
the centroid motion has been reduced by a factor of ![]() , and the
power due to the periodic error no longer dominates the centroid motion.
, and the
power due to the periodic error no longer dominates the centroid motion.
 |
A long term problem with UKIRT's tracking performance has been investigated and successfully solved. Whilst most observations do use the autoguider, this fix has been enormously successful at times when this proves impossible. For example, the ex Head of UKIRT (who should know!) penned the following words in a recent observers report:
``On Jupiter and Saturn we could not autoguide, but the much improved tracking (finally free from RA wobble) effectively has improved the angular resolution of our measurements on these planets by a factor of. This is a great improvement and we send our compliments to the team that finally accomplished this.''
What more can we say?
Pearson, E., Kansky, M., & Tobey, N. 1990, Presentation of 24 bit optical encoder system. unpublished material, BEI Motion Systems Company