The nature of the HST/WFPC2 point-spread function (PSF) is such that
is is (1) under-sampled by factors of 2 to 4 (Biretta et al. 1996);
(2) spatially varying over the field of view (FOV) due to
field-dependent aberrations etc.; and (3) characterized by
considerable high-frequency structure in the ``wings" (
![]() FWHM). As a result, residuals from determining
& fitting the PSF to the image appear much larger than with
well-sampled images, making it difficult to cleanly subtract stars
which are ``neighbors" to the PSF stars; while around bright stars,
both these residuals and the high-frequency structure in the PSF wings
resemble faint stars, thus causing errors in star detection (either
missed detections of real objects, or false detections of ``starlike"
artifacts). Finally, under-sampling reduces the statistical accuracy
of the fit, and fitting many thousands of overlapping star images
simultaneously is a computing resources (memory & CPU) problem unless
compromises are made with sub-groupings; so for these reasons some
system involving aperture photometry would be more desirable, but
crowding does not permit this.
FWHM). As a result, residuals from determining
& fitting the PSF to the image appear much larger than with
well-sampled images, making it difficult to cleanly subtract stars
which are ``neighbors" to the PSF stars; while around bright stars,
both these residuals and the high-frequency structure in the PSF wings
resemble faint stars, thus causing errors in star detection (either
missed detections of real objects, or false detections of ``starlike"
artifacts). Finally, under-sampling reduces the statistical accuracy
of the fit, and fitting many thousands of overlapping star images
simultaneously is a computing resources (memory & CPU) problem unless
compromises are made with sub-groupings; so for these reasons some
system involving aperture photometry would be more desirable, but
crowding does not permit this.
To overcome the problems outlined above when performing photometry in the dense core fields of globular clusters, a new approach was developed. The HST/WFPC2 images were pre-processed using the Maximum Entropy Method (MEM) for image deconvolution (Narayan & Nityananda 1986, Skilling & Bryan 1984). One would expect improved star detection on sub-sampled MEM - deconvolved images, because the actual complex HST PSF shape is used in the star detection process via MEM, which effectively ``Gaussianises" the PSF, doubles the sampling, and better separates the stars from each other. This work also compared aperture photometry on the sub-sampled MEM-deconvolved images to the following conventional reductions of the original data: aperture photometry, profile-fitting photometry, and the hybrid method (e.g. Yanny et al. 1994) of aperture photometry on neighbor-subtracted images.
The first PSF model for each WFPC2 chip & filter combination had to
be 2![]() sub-sampled, quadratically variable in a spatial sense, and
a good match to the real PSF. A 6
sub-sampled, quadratically variable in a spatial sense, and
a good match to the real PSF. A 6![]() 6 grid of normal-sampled
Tiny Tim (Krist & Hook, 1996) synthetic PSFs provided the ``stars''
from which DAOPHOT-II (Stetson 1994) computed this model PSF.
But in the STSDAS implementation of MEM, the PSF must be
spatially-invariant, so deconvolution was performed on a 6
6 grid of normal-sampled
Tiny Tim (Krist & Hook, 1996) synthetic PSFs provided the ``stars''
from which DAOPHOT-II (Stetson 1994) computed this model PSF.
But in the STSDAS implementation of MEM, the PSF must be
spatially-invariant, so deconvolution was performed on a 6![]() 6
grid of highly overlapping 256
6
grid of highly overlapping 256![]() 256 pixel sub-images, each with
its own PSF appropriate to that position on the chip. The deconvolved
sub-images were then reassembled into a sub-sampled whole, upon which
the star detection (using DAOPHOT-II/DAOFIND) and photometry
steps were performed. Coaddition of deconvolved images in two bands
(F555W and F814W), with a moderate rejection threshold for
statistically deviant positive features, greatly suppressed
deconvolution artifacts around the brighter stars1. Coadding also provided slightly
greater depth. After a first DAOPHOT-II/ALLSTAR PSF-fit of the
original images, a new sub-sampled, quadratically variable model was
empirically computed from
256 pixel sub-images, each with
its own PSF appropriate to that position on the chip. The deconvolved
sub-images were then reassembled into a sub-sampled whole, upon which
the star detection (using DAOPHOT-II/DAOFIND) and photometry
steps were performed. Coaddition of deconvolved images in two bands
(F555W and F814W), with a moderate rejection threshold for
statistically deviant positive features, greatly suppressed
deconvolution artifacts around the brighter stars1. Coadding also provided slightly
greater depth. After a first DAOPHOT-II/ALLSTAR PSF-fit of the
original images, a new sub-sampled, quadratically variable model was
empirically computed from ![]() 90 - 100 bright stars. This second,
refined PSF was then used to repeat the MEM deconvolution and
PSF-fitting steps.
90 - 100 bright stars. This second,
refined PSF was then used to repeat the MEM deconvolution and
PSF-fitting steps.
 |
In addition to testing these procedures on the real HST/WFPC2 data of
the Milky Way bulge globular cluster NGC 6293 in the F555W and F814W
bands, other cluster images were simulated in order to quantify the
photometric and astrometric performance of the technique. These are
the simulated images specifications: 19957 input stars (17175 centred
within the FOV); Trager et al. (1995) NGC 6293 spatial distribution
(modified for a steeper form in the core); Z=0.0040, Y=0.24, Age=14
Gyr isochrone/luminosity functions of Bertelli et al. (1994); Janes
& Heasley (1991) NGC 6293 apparent distance modulus (=16.0); Holtzman
et al. (1995) and Whitmore (1995) HST zeropoints & photometric
system calibrations; same net gain, readnoise, exposure time,
saturation level, and mean background as the NGC 6293 images;
2![]() -sub-sampled, spatially varying DAOPHOT-II model of a
Tiny Tim grid for input PSF with 0".015 rms pointing-jitter.
-sub-sampled, spatially varying DAOPHOT-II model of a
Tiny Tim grid for input PSF with 0".015 rms pointing-jitter.
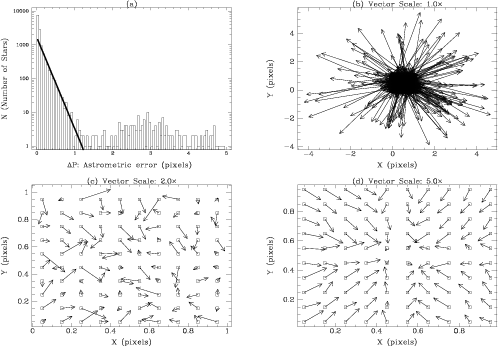 |
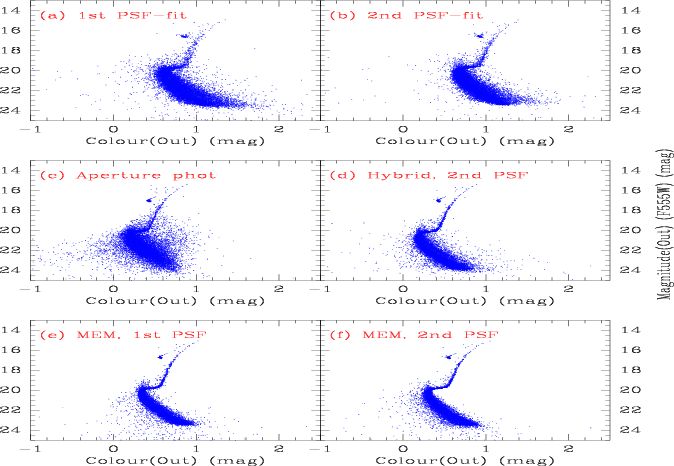
Figure 1 shows the photometric results for the simulated
images and Figure 2 shows their astrometric
results. Star detection rates were indeed improved: 9446 stars were
found with conventional methods, but 13528 stars with
MEM-preprocessing. The improvement in the photometric accuracy was
more moderate. In terms of random colour deviations from the ``truth''
input values, aperture photometry on the subsampled MEM-deconvolved
images was on a par with the hybrid method for bright objects, and
somewhat better for faint objects, thus statistically better overall.
NGC 6293 showed similar improvements. In Figure 2(a),
78% of all the detected stars have astrometric accuracies better than
0.1 pixels (bins 1-2); there is a power law decline due to noise (fit
overplotted) from bin 3 onwards. Note the clear sub-pixel pattern in
Figure 2(d): this indicates that systematic errors are
induced at a level ![]() 0.1 pixel; this is fine for the purpose of
crowded-field photometry, but precludes the use of this technique for
high-precision astrometry. The deconvolution algorithm used should not
matter, once it supports subsampling and the Poisson photon-counting
and Gaussian read-out noise sources. Newer algorithms (e.g. Magain et
al. (1998), which handles sampling correctly) may improve results
further.
0.1 pixel; this is fine for the purpose of
crowded-field photometry, but precludes the use of this technique for
high-precision astrometry. The deconvolution algorithm used should not
matter, once it supports subsampling and the Poisson photon-counting
and Gaussian read-out noise sources. Newer algorithms (e.g. Magain et
al. (1998), which handles sampling correctly) may improve results
further.
This research was supported by the TMR programme of the European Commission (contract ERBFMBICT972185). I am also grateful to my Edinburgh host, Prof. Douglas Heggie, Dr. Andy Shearer & Dr. Aaron Golden (NUI Galway, Ireland) and Dr. Alan Penny (RAL, UK) for their advice and encouragement.
Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&A, 106, 275
Biretta, J. A., et al. 1996, WFPC2 Instrument Handbook, Version 4.0 (Baltimore: STScI)
Holtzman, J., et al. 1995, PASP, 107, 1065
Janes, K. A., & Heasley, J. N. 1991, AJ, 101, 2097
Krist, J., & Hook, R. 1996, Tiny Tim User's Manual, V4.2 (Baltimore: STScI)
Lindler, D., Heap, S., Holbrook, J., Malumuth, E., Norman, D., & Vener-Saavedra, P. C. 1994, in The Restoration of HST Images and Spectra II, ed. R. J. Hanisch & R. L. White (Baltimore: STScI), 286
Magain, P., Courbin, F., & Sohy, S. 1998, ApJ, 494, 472
Narayan, R., & Nityananda, R. 1986, ARA&A, 24, 127
Skilling, J., & Bryan, R. K. 1984, MNRAS, 211, 111
Stetson, P. B. 1994, PASP, 106, 250
Trager, S. C., King, I. R., & Djorgovski, S. 1995, AJ, 109, 218
Whitmore, B. 1995, in Calibrating Hubble Space Telescope: Post Servicing Mission, (Baltimore: STScI)
Yanny, B., Guhathakurta, P., Schneider, D., & Bahcall, J. 1994, ApJ, 435, L59