 |
AST uses object-oriented concepts, but may be called from standard C and FORTRAN (it is implemented in ANSI C). The initial implementation was described at the ADASS '97 meeting (Warren-Smith & Berry 1998). This paper describes some more recent new features.
 |
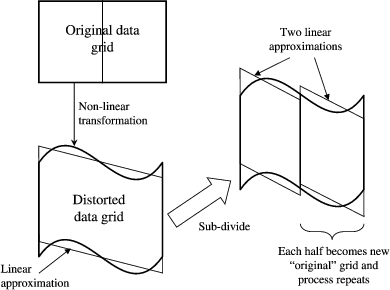
AST first approximates a non-linear transformation with a simple linear one. If this matches the true transformation sufficiently accurately, it is used, being fast to compute. Otherwise, the image is sub-divided along its largest dimension and a new linear approximation is found inside each half of the image. Sub-division continues until a sufficiently accurate piecewise linear approximation has been found. The algorithm adapts rapidly to non-linearity, so as to minimize the number of true transformation evaluations needed. This process is illustrated in Figure 2.
 |
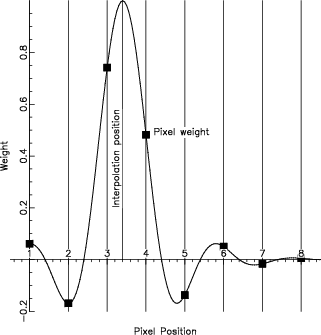
Sub-pixel interpolation between data values may also be required if the transformed pixel positions are not at integer-valued locations. AST supports a variety of interpolation methods based on weighted sums of nearby pixels. You can also provide your own interpolation function. AST's built-in weighting kernels include the popular linear-interpolation and nearest-neighbor schemes, as well as sinc, sinc xsinc, sinc xcos and sinc xgaussian variants (e.g. Figure 3), which are suitable for well-sampled data. Missing data can also be accommodated.
 |
All of these re-sampling algorithms are available in 1, 2, 3 or more dimensions via a single function call.
In practice, therefore, AST is now able to read/write most available FITS headers which describe coordinate systems.
The first approach allows a function written in C or FORTRAN to be packaged as an AST object (a form of Mapping). It may then participate in any AST operation, such as image re-sampling or generation of graphical output. This allows a programmer great freedom in defining new coordinate transformations. However, since it requires linking with locally-compiled code, it cannot describe coordinate systems in a transportable manner.
To overcome this, the latest version of AST (V1.4) contains an expression parser which can interpret transformations expressed in mathematical notation at run-time. A range of operators and mathematical functions are provided, so that C code such as the following can be used to define new transformations (note how the transformation is actually 2-dimensional, but a number of intermediate results are first computed):
char *forward[] = { "rin = sqrt( XIN * XIN + YIN * YIN )",
"rout = rin * ( 1 + 0.1 * rin * rin )",
"theta = atan2( YIN, XIN )",
"XOUT = rout * cos( theta )",
"YOUT = rout * sin( theta )" };
char *inverse[] = { "rout = sqrt( XOUT * XOUT + YOUT * YOUT )",
"r = rout / 0.2",
"d = sqrt( 1 / 27e-2 + r * r )",
"rin = pow( d + r, 1/3 ) - pow( d - r, 1/3 )",
"theta = atan2( YOUT, XOUT )",
"XIN = rin * cos( theta )",
"YIN = rin * sin( theta )" };
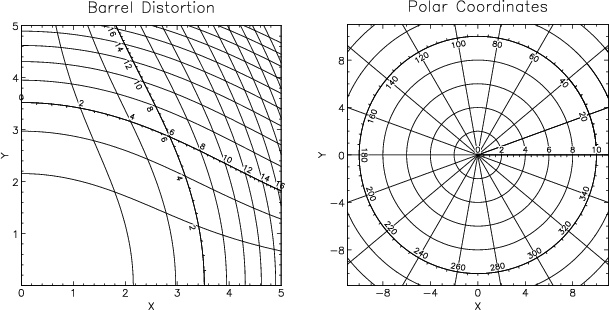
A constructor function is then called to compile these arrays into a new AST object (a MathMap) which, in this case, describes barrel distortion. Shown in Figure 4 (left) is an example of a coordinate grid drawn automatically by AST for this transformation. Note that AST has no built-in knowledge about this coordinate system, beyond the equations above. These might, for example, have been obtained from FITS headers. A similar example using polar coordinates is also shown (Figure 4, right).
 |
Warren-Smith, R. F & Berry, D. S. 1998, in ASP Conf. Ser., Vol. 145, Astronomical Data Analysis Software and Systems VII, ed. R. Albrecht, R. N. Hook, & H. A. Bushouse (San Francisco: ASP), 41