 |
The initial paper describing the Flexible Image Transport System, or FITS format (Wells, Greisen, & Harten 1981) proposed keywords to describe the physical coordinates of image data. The original authors chose to defer discussion of the technical details of coordinate specification until the basic FITS format was accepted generally and until a deeper understanding of image coordinate specification and computation could be obtained. While participating in the development of the AIPS software package of the National Radio Astronomy Observatory, Greisen (1983) developed FITS-like syntax and semantics to define both velocity and celestial coordinates. The latter have been widely used for interchanging imagery from a number of instruments at widely differing spectral domains and form the basis of the present proposal. That proposal is presented in three papers which are available from our WWW home pages: 3
| 1. | Representations of world coordinates in FITS |
| by Greisen and Calabretta (general conventions, units) | |
| 2. | Representations of celestial coordinates in FITS |
| by Calabretta and Greisen (celestial projections) | |
| 3. | Representations of spectral coordinates in FITS |
| by Greisen (spectral and velocity axes) |
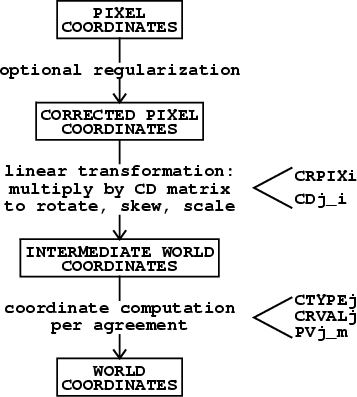
The computation of the coordinates associated with each pixel is broken into three steps, a correction for arbitrary small image distortions, a linear transformation (including rotation, scale and skew), and transformation from intermediate world coordinates to the required world coordinate system via a predefined algorithm. These steps and the FITS header keywords used to define them are illustrated in Figure 1. The pixel regularization correction is encoded in an image extension and accounts for small distortions which can't easily be described by other means. It will often be omitted by FITS writers and may be ignored when present by many FITS readers. The linear transformation is done with a translation specified by the familiar CRPIX i followed by a matrix multiplication specified by CD j_ i keywords. The resulting ``intermediate world coordinates'' are in physical units (e.g., deg, m/s), but require conversion via a predefined linear or non-linear algorithm into the final world coordinate system. The algorithm and final coordinates are selected by the two halves of the CTYPE j header keywords, parameters are given via the CRVAL j and, if needed, PV j_ m keywords, and the units are specified with CUNIT j keywords. Additional header keywords may be defined as needed to further describe the coordinates. The old CDELT i and CROTA i header keywords are no longer used. The coordinates for integer voxel numbers refer to the center of the voxel, the only location within an individual voxel that is invariant to rotation and transposition.
In some cases, an image may be described by more than one set of coordinates. For example, spectral axes may be described by frequency, wavelength, and velocity (only one of which might be linear) and spatial axes may be described, for example, by position in the telescope focal plane in meters as well as in degrees on the sky. To permit up to 26 secondary coordinate descriptions, a version code may be appended to each of the standard header keywords (e.g., CRVAL27Q). These codes are the letters A through Z, with the blank character being reserved for the primary version. If an alternate coordinate description is specified, all coordinate keywords for that version must be given even if they do not differ from those of the primary version. Note that this convention (and the CD j_ i keyword) reduce the maximum axis number from 999 to a more reasonable 99.
Paper I contains a detailed proposal for a new IAU standard for the representation of units when they must appear in plain character form. This proposal is a merger and clarification of the systems devised by George & Angelini (1995) and Ochsenbein et al. (1996) and is a supplement to the IAU Style Manual (1988) which defines units as they would appear in a published document.
Image data are represented in FITS not only in the primary array and in an IMAGE extension, but also in a multi-dimensional vector in a single element of a FITS binary table and a tabulated list of pixel coordinates in a FITS ASCII or binary table. Keywords to specify the coordinates of such data are given in appendices to Papers I, II, and III and, for the primary coordinate description, match those already in use by some software systems.
Paper II applies the general formalism of Paper I to the problem of representing celestial coordinate systems. With detailed mathematical formulæ, it covers all (24) spherical map projections likely to be of interest in astronomy including zenithal, cylindrical, pseudo-cylindrical, conic, polyconic, pseudo-conic, and quad-cube projections. The familiar gnomonic or `` -TAN'' projection is extended to allow up to 80 parameters to describe a full astrometric solution to the distortions in a photographic or CCD image. The projections support terrestrial and planetary mapping as well as celestial mapping. Several examples of header interpretation are provided and header construction is exemplified by cases taken from full-sky imagery, the Digitized Sky Survey, a long-slit spectrograph image, and an image of the Moon. The major celestial coordinate systems are supported including generalized longitude-latitude pairs and a new keyword RADECSYS is defined to specify the coordinate system (i.e. 'FK4', 'FK5').
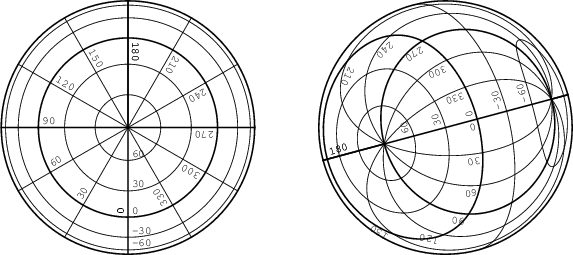
In the computation of celestial coordinates, ``intermediate world coordinates'' are identified with Cartesian coordinates in the plane of projection. The computation of world coordinates then requires first de-projection of the Cartesian coordinates to obtain ``native spherical coordinates'' and then spherical coordinate transformation with rotation angles defined by CRVAL j and new LONPOLE and LATPOLE keywords. The native coordinate system is the one in which the projection is most conveniently defined and the reference values in the desired system must correspond to the ``reference point'' of the projection. This is fixed for each class of projection. Oblique projections are generated naturally in this fashion as illustrated in Figure 2.
The coordinates of Paper II are supported by the WCSLIB software package (Calabretta 1999) available without charge under GNU licensing.
 |
Paper III extends the methods of Papers I and II to represent frequency, wavelength, and velocity including the radio, optical and redshift conventional velocities. Conversion formulæ for data measured in any one of these and expressed in any one of these are given. Provision is made for higher order pixel corrections. Keywords are defined to specify velocity coordinate reference frames and any parameters needed to switch between them. Methods to describe the dependence of spectral coordinates on celestial coordinates are given for velocity reference frames and for instruments similar to Fabry-Perot interferometers. It is noted that objective prism data, in which one spectral and two spatial axes are mingled on a two-dimensional image, cannot be described by the methods of Papers I and III. When these data are reduced to tabular form, they are easily described by the conventions presented in all three papers for such data.
Calabretta, M. 1999, WCSLIB, Version 2.4, located at
ftp://ftp.atnf.csiro.au/pub/software/wcslib/wcslib.tar.gz.
George, I. M. &Angelini, L. 1995, Specification
of Physical Units within OGIP FITS files, OGIP Memo OGIP/93-001,
NASA Goddard Space Flight Center, Greenbelt, Maryland,
ftp://fits.cv.nrao.edu/fits/wcs/OGIP93_001.ps
Greisen, E. W. 1983, AIPS Memo No. 27, National Radio Astronomy Observatory, Charlottesville, Virginia
IAU Style Manual 1983, IAU Inf. Bull., No. 49, 14.
Ochsenbein, F., Paul, N., & Kuin, M. 1996, Standards for Astronomical Catalogues, Version 1.5, http://vizier.u-strasbg.fr/doc/catstd.htx
Wells, D. C., Greisen, E. W., & Harten, R. H. 1981, A&AS, 44, 363