 |
The current trends in astronomy require essential improving the resolution and broadening the spectral range of imagery acquired by space borne instruments. Better productivity of space observations yields enormous growths of data volumes that causes a serious technical problem of reducing the increase in data storage and space transmission costs. As it is not uncommon for multispectral/hyperspectral remote sensing, a typical data set for a single frame of imagery may occupy a few gigabytes of space. The onboard compression can allow to essentially unload the data transmission channels, as well as enable more efficient data storage and processing.
Most of the existing effective image encoding techniques designated to still image compression are not suitable to parallel operation and often fail with large real images, as they assume loading the entire image or its significant portion into the memory and usually have fairly high demand to the onboard computer performance and storage media capacity. The state of the art transform-based techniques, including wavelet and fractals, implicate complex mathematical transformations involving every pixel of the image, thus resulting in very active CPU use. High speed readout processing, which is crucial for very dense inputs, can also be hardly attainable with these techniques. The existing real-time encoding schemes, allowing incremental image compression, like those implemented in CCITT/ITU-T telecommunication coding standards, are usually behind the leading still image compression techniques. They rarely give a compression factor of more than 10 in the lossless mode, and still do not give satisfactory speed performance with the high-resolution imagery.
In this paper we describe an attempt to implement a simple and robust compression algorithm, which would combine reasonable compression rate and high coding speed to be suitable for real-time processing the large images.
The discussed technique is designed to be most efficient for compressing the bitonal imagery, however, like many other bitonal compression schemes, its application range can be extended to other image types. Unlike most leading bitonal image compression techniques being currently in use that implement direct bit map compression across the raster lines with run-length, arithmetic or other coding schemes, the contour-based technique embodies another approach. It exploits spatial information redundancy, which resides in most real images, and takes advantage of replacing the regions of adjacent pixels with the same either color or classification characteristics by their contours, thus eliminating this redundancy. The approach allows efficient and fast one- stage compression through image decomposition into a set of contours and binding the contours in the chain link bit-flow, thus storing only those bits belonging to the contours.
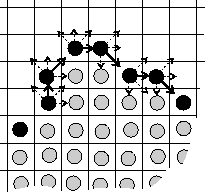
Contour recording is performed through detection of each contour and sequential coding the relative coordinates of the contour pixels exploiting their continuity and logical linking. Obviously, every successive move along the contour line can be completely defined by only three bits. To achieve better compression, some additional logical restrictions to the possible moves can be applied, so that only two bits per pixel may be used providing virtually lossless compression. In this case a minimum buffering is required to keep the previous running coordinate for each contour pixel. Figure 1 illustrates contour recording with restrictions based on the previous contour pixel coordinates and clockwise contour bypass rule. As a result of encoding, the contours represented in the original bitmap become stored in the one-dimensional bit sequence. The contour entry coordinates can be stored either separately or in the resulting bit flow.
 |
Actual implementation of the contour-based compression algorithm implicates simultaneous edge detection and storage without the need of preliminary image contouring. Our algorithm compresses images line by line and handles only current relative positions on particular edges at a time, so that the resulting bit flow is shaped by sliding the current bypass point along the successive edge pixels of the image regions with same attribute pixels. Therefore we also call this algorithm and general approach as Running Edge Image Compression (REIC).
The REIC implementation for compressing the grayscale and color images assumes performing the Gray coding (Gray 1953) and bit plane separation first and, then, passing each plane to a separate instance of the algorithm (see, e.g., Abdat & Bellanger 1994 for an example of Gray/bilevel coding combination). An alternative approach assumes assigning the classification codes based on image color mode and bit- depth to each contour object with subsequent storage of the codes in the compressed bit sequence.
We performed the preliminary comparative tests of the contour-based compression technique with the high resolution bitonal images. Our tests have shown that, in the two bits per pixel mode, the contour-based encoding combined with the generic GZIP encoding gives about 30 per cent better compression for still 600 dots per inch images to the widely used CCITT/ITU-T Group 4 and about three times to Group 3 compression standards. Application of the REIC technique alone gives near-equal compression to Group 4, however, results in several times higher encoding speeds. The intrinsic nature of the contour-based compression allows to utilize mathematical logic for edge detection and contour encoding rather than arithmetic operations whenever possible, thus reducing the CPU use and approaching the ultimate speed performance. Higher resolution images allow for increasingly better compression.
While implementation of the REIC technique steadily exhibits good compression in our tests with a variety of bitonal images, its efficiency for other kinds of imagery is essentially determined by image type and nature. Among the factors affecting the contour-based compression, most important are image noisiness and complexity. When compressing color imagery, the color depth puts additional limits to REIC efficiency. Our tests gave satisfactory results with high-resolution noise-free images of up to 8 bits per pixel.
Scanning line operation of the REIC allows it to be conjoined well with the spectral compression technique proposed by the author earlier (Vasilyev 1998), and these two techniques can be concurrently implemented for efficient onboard multispectral/hyperspectral image compression.
Lossy version of the REIC technique assumes sparse representation of contours first, thus providing additional compression, and then coding the contours in an ordinary way. In this scheme, the image decompression is performed beginning with interpolation of the contours. Such a lossy-type scheme can be customized and optimized for different applications to achieve maximum compression ratio with negligible visual degradation of the image. It also should not significantly affect the coding speed, since the required transformations will be applied to only contour pixels. In a lossy mode, the resulting bit flow will have longer continuous sequences of the same bits, thus giving some additional compression opportunity for subsequent application of other coding schemes. It should be noted that the lossy REIC belongs to nondegrading methods, and, as once applied, its repeated application to the same image does not lead to any further change to the image.
The operation principles of the contour-based compression allow to encode images in the scanning-line mode that makes the technique applicable to the real time image processing systems and on board compression. The approach allows sequential encoding of images of virtually any size including multispectral and hyperspectral imagery, while consuming small amount of RAM memory and operating in a computationally inexpensive way with no need for special hardware. The method can be promisingly efficient for automatic-mode high-resolution color image recording and mapping when combined with the pattern recognition and edge detection techniques. It can also be suitable for document imaging and sending imagery applications.
The author is grateful to the ADASS VIII Organizing Committee and European Southern Observatory for offering him the financial assistance to attend the Conference.
Abdat, M. & Bellanger, M. G. 1994, in Proc. IEEE First Intl. Conf. on Image Processing, 3, 851
Gray, F. 1953, U.S. Patent 2632058
Vasilyev, S. 1998, in ASP Conf. Ser., Vol. 145, Astronomical Data Analysis Software and Systems VII, ed. R. Albrecht, R. N. Hook, & H. A. Bushouse (San Francisco: ASP), 504