| Simplex | Powell |
| Grid | Grid + Powell |
| Monte Carlo | Monte Carlo + Powell |
| Simulated Annealing 1 | Simulated Annealing 1 + Powell |
| Simulated Annealing 2 | Simulated Annealing 2 + Powell |
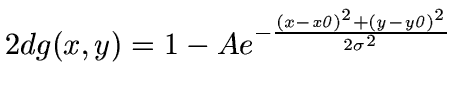 ,
,
![]() ,
,
![]()
![]()
The function ![]() has coefficients si, ti, di, and c
defined such that the function is a
paraboloid with axes parallel to the coordinate axes, and a
set of holes that increase in depth near the origin. The
function is very difficult to
minimize, having over 1020 local minima in which the
optimization may become trapped:
has coefficients si, ti, di, and c
defined such that the function is a
paraboloid with axes parallel to the coordinate axes, and a
set of holes that increase in depth near the origin. The
function is very difficult to
minimize, having over 1020 local minima in which the
optimization may become trapped:
![]() if
if
![]()
![]()
![]() otherwise,
otherwise,
![]()
si=0.2,ti=0.05,i=1,....4,
![]()
c=0.15,
![]()
The function f1 is a simple sum of squares, with a
single minimum:
![]()
The function f2 is the classical Rosenbrock function:
![]()
The function f3 is discontinuous and has a single minimum:
![]()
The function f4 is a noisy function, as ![]() is a
uniform random variable bounded by
is a
uniform random variable bounded by
![]() :
:
![]()
Function f5 has 25 local minima, and is optimized
with a value of approximately
0.001996 when
x1=x2=-32:
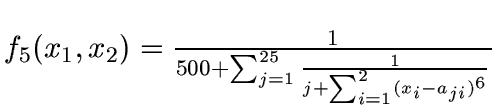
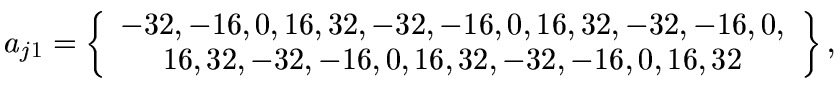
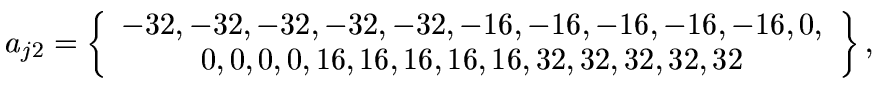
![]()
Table 1 summarizes the results for scenario B. For each
function and technique, the value shown is the normalized
final parameter distance, defined as the ratio of the
distance between the final parameter state and the global
minimum to the maximum distance between any
two states within the allowed parameter space. Distances of
less than 10-6 are shown as 10-6. In general, the
results for scenario C (not shown) indicate that, as expected, a more
favorable initial state improved the
single-shot routines' optimizations of smoothly varying
functions. The final column is the execution time for the
gaussian, normalized to the time for the simplex method. The
result of one technique is plotted in Fig.
1, with the initial parameter distances for scenarios A, B
and C.
Using optimization scenario C, the global minimum was located for all
functions except ![]() , in which the routines became
trapped in local minima. For this function, the grid
and simulated annealing
techniques would presumably locate the minimum if strict enough criteria were
used; the grid method showed improved optimization for
scenario B compared to scenario A. Ingber & Rosen (1992) tested
a similar function with 30 variables and obtained
comparable results.
, in which the routines became
trapped in local minima. For this function, the grid
and simulated annealing
techniques would presumably locate the minimum if strict enough criteria were
used; the grid method showed improved optimization for
scenario B compared to scenario A. Ingber & Rosen (1992) tested
a similar function with 30 variables and obtained
comparable results.
The single-shot routines successfully converged for the smoothly varying functions (2dg, f1, and f2), particularly when starting from a favorable parameter state. For the discontinuous functions, these routines sometimes became trapped in local minima. In these cases, the optimizations were not improved substantially by using an initial parameter state closer to the global minimum or by using stricter convergence criteria.
The scatter-shot routines were less successful in optimizing the smooth functions, as they sample the entire parameter space without refining the search near the minimum. However, for both the smooth and the discontinuous functions, the addition of the Powell technique improved the optimization, at the expense of longer execution times (see Table 1). Such methods with refining steps following sampling of the parameter space are to be preferred.
This project is supported by NASA contract NAS8-39073. I would like to thank the following individuals for helpful discussions and their review: Mark Birkinshaw, Janet DePonte, Stephen Doe, Diab Jerius, Malin Ljungberg, Dan Nguyen, Aneta Siemiginowska, and Robert Zacher.
Birkinshaw, M. 1998, Some Advice on Minimization Routines, (AXAF Science Center Internal Memo)
Doe, S., Ljungberg, M., Siemiginowska, A., & Joye, W. 1996, in ASP Conf. Ser., Vol. 145, Astronomical Data Analysis Software and Systems VII, ed. R. Albrecht, R. N. Hook, & H. A. Bushouse (San Francisco: ASP), 157
Ingber, L. & Rosen, B. 1992, Mathematical and Computer Modelling, 16(11), 87
More, J., Garbow, B. S., Hillstrom, K. E. 1981, ACM Trans on Math. Software, 7, 17