| d(Sx,Sy,n) | = | 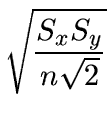 |
(1) |
Jitter imaging is an efficient method used in astronomical infrared observations to take care of sky background issues with a minimum loss of observing time. By observing the same spot on the sky with small offsets around a central position for each exposure, it is hopefully possible to deduce the sky background variations directly by filtering the images, and to separate the astronomical and the sky signals.
A typical acquisition in jitter mode consists in a set of 10 to 100 frames. The first frame is assumed to be centered on the point of interest; the following frames are slightly offset from the first position with offsets no larger than a reasonably small fraction of the detector size (15% for SOFI/ISAAC). The data reduction process consists of sky estimation and subtraction, plane recentering, and finally frame co-addition to a single frame. Each processing step is discussed here in the context of automatic data reduction in pipeline mode (i.e., without user interaction).
The following procedure is used to generate homogeneous offsets to use for a standard jittered observation. Points are generated with a Poisson sampling law (Wolberg 1990) which specifies that no two points are closer to each other than a minimal distance. This distance is computed by taking into account the size of the (rectangular) domain in which points are generated, and the number of points to generate. The minimal distance between any two points for a set of n points generated in a rectangle of size Sx x Sy is chosen as:
| d(Sx,Sy,n) | = | 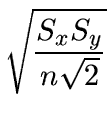 |
(1) |
Sky background filtering is done through a method called sky combination. The method is an iteration on each pixel position on the detector along a time line. The algorithm can be described for each pixel position as:
Notice that if rmin = rmax = h, this method is equivalent to a running median filter; only the central sorted value is kept.
The next step is to measure or acquire the offsets between the frames. It is reasonable to assume that the acquisition orders for telescope pointing are available as ancillary data. If they are not, there should be an automatic way of finding these offsets with a minimal chance of error. Lastly, users may want to use their own method to detect offsets and feed their input into the algorithm for ultimate refining. We discuss here a cross-correlation method used both for automatic offset detection and refining up to subpixel resolution.
Cross-correlation techniques need valid points in the image to work properly. We describe here a simple peak detector used to detect such points. In most cases, it should provide a reasonable number of points to use for offset detection.
Create a binary image from the input frame by thresholding with a
![]() clipping. Instead of using mean and sigma values for this
clipping, we estimate these values with a median and average
absolute deviation from the median, to be less sensitive to noise.
clipping. Instead of using mean and sigma values for this
clipping, we estimate these values with a median and average
absolute deviation from the median, to be less sensitive to noise.
The value of K depends on the amount of noise and the number of objects present in the image. For very noisy images, it is best to lower K to a value between 0.1 and 1 (the default is 3).
This thresholding creates a crude map of bright regions in the input image. To clean bad pixels and other such small defects, a binary morphological erosion is then performed. A classical floodfill algorithm is then applied to estimate the centroid of each remaining region, weighted by pixel values of the input image. A list of detected object centers and maximum pixel values in each region is then returned.
The cross-correlation of two images I1 and I2 is defined as the product:
| (2) |
where p1 is the pixel value which index is running over the domain of interest w1 in the image I1, and similarly p2 a pixel value which 2-dimensional index is running over the domain of interest w2 in the image I2. The cross-correlation product we use is a sum of squared differences:
| (3) |
With this criterion, the point of greatest similarity corresponds to a minimum of difference in the cross-correlation product. A subpixel offset detection is then applied by fitting a parabola to the cross-correlation signal in x and y, and looking for the subpixel minimum. This method is theoretically precise up to a 1/100 pixel precision in the ideal case of noiseless images. The precision obtained with SOFI data is about 1/10 pixel.
In automatic mode when there is no indication of what the offsets between frames are, this cross-correlation technique is used within a wide search zone. When a first estimate of the offsets is available (refining mode), the search area is lowered to a few pixels in all directions to speed up the process.
To shift an image by a subpixel offset, it is necessary to use resampling methods. Given some assumptions about the input signal cut-off frequency, an image is considered as the discretization of a continuous band-limited signal. According to Shannon's theorem, it is possible to completely retrieve this continuous signal given enough samples. It is then easy to resample the image, i.e., to construct a new image with samples taken at a new position of interest, namely the required offset. Interested readers are referred to Wolberg (1990).
In the present implementation, we chose to resample images in the image space. The interpolation kernel is based on the 16 closest pixel values, and the kernel definition is based on a hyperbolic tangent function in Fourier space:
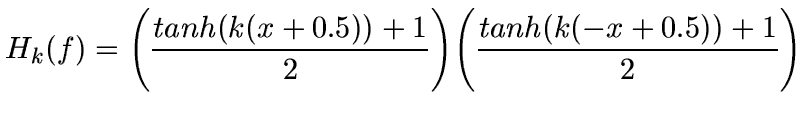 |
(4) |
This interpolation kernel is then computed in image space through a Fourier transform. It converges exponentially toward zero, which makes it an ideal candidate for resampling with a small pixel neighborhood.
The last step of the reduction is to concatenate all registered planes on the third axis into a single plane. The method we use is a filtered 3D average. For each pixel position, we reject outliers along the time axis and average remaining pixels to a single value. This yields the single output frame, which is the result of the data reduction process.
Interested readers are referred to a more complete ESO document at http://www.eso.org/projects/dfs/papers/jitter98/. The eclipse library has been used to implement this algorithm. The home page for this software package can be found at http://www.eso.org/eclipse.
Wolberg, G. 1990, Digital Image Warping, (Los Alamitos: IEEE Press)