Next: The Co-Addition Technique Applied to Images of Galaxy Cores
Up: Applications
Previous: Slitless Multiobject Spectroscopy with FOSC Type Instruments
Table of Contents -- Index -- PS reprint -- PDF reprint
Nailong Wu and John Caldwell
Dept. of Physics and Astronomy, York University,
4700 Keele St., North York, Ontario, M3J 1P3, Canada
The substepping technique is used to ameliorate the problem of undersampling in data acquisition for an imaging system. For the HST, undersampling means that the size of the pixel in a camera is larger than the critical value determined by the optics of the telescope, and aliasing takes place.
Obviously, the problem of undersampling could be resolved if the pixel size could be reduced. However, in many circumstances, the pixel size is fixed. Then, substepping is the only solution to the problem. In essence, substepping means that data are acquired in steps smaller than the pixel size, and then processed to achieve resolution comparable to the step size.
In this section one-dimensional (1-D) notation and diagrams are used for clarity. Results can be easily extended to the two-dimensional (2-D) case by changing dimensional subscripts and operations to 2-D.
Sampling is an operation to integrate a(x) within a pixel, and to assign the result to this pixel (Figure 1A). Each pixel has its nominal position at the center of the integral interval.
To avoid aliasing, the sampling interval ![]() must be equal to (critical sampling) or smaller than (oversampling)
its critical value
must be equal to (critical sampling) or smaller than (oversampling)
its critical value ![]() ,which is determined by the
highest frequency component in a(x).
If
,which is determined by the
highest frequency component in a(x).
If ![]() (undersampling),
aliasing will take place.
(undersampling),
aliasing will take place.
In order to overcome the problem of undersampling (Figure 1A),
we may reduce the pixel size by a factor of N, such that
![]() (proper sampling, including critical sampling and oversampling;
Figure 1D for N=2).
We call this normal sampling because both the integral and sampling
intervals are equal to the pixel size.
(proper sampling, including critical sampling and oversampling;
Figure 1D for N=2).
We call this normal sampling because both the integral and sampling
intervals are equal to the pixel size.
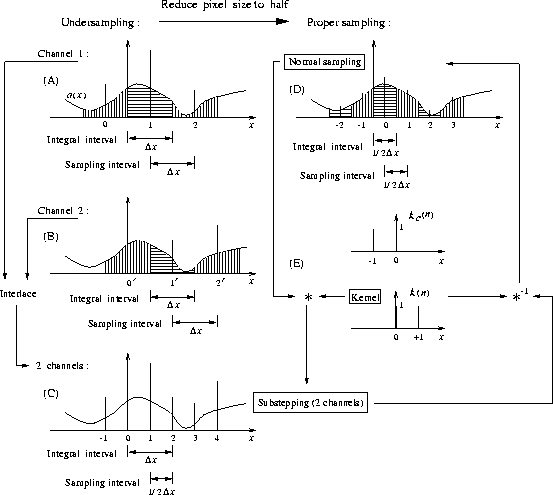 |
In the case where reducing the pixel size is impossible,
we can use N integral-sampling devices (channels)
to acquire data.
The resulting N sequences shifted successively by ![]() (Figure 1A,B)
are combined in a manner of interlacing (C), so that the
sampling interval becomes
(Figure 1A,B)
are combined in a manner of interlacing (C), so that the
sampling interval becomes ![]() .We call this subsampling or substepping
because the sampling interval is equal to a subpixel size
while the integral interval is still equal to the pixel size.
If N is sufficiently large such that
.We call this subsampling or substepping
because the sampling interval is equal to a subpixel size
while the integral interval is still equal to the pixel size.
If N is sufficiently large such that ![]() ,
aliasing will be eliminated, and
consequently resolution will be improved.
,
aliasing will be eliminated, and
consequently resolution will be improved.
Let us compare substepping (Figure 1C) with normal sampling (D),
both with the sampling interval ![]() .For the former, the integral interval is larger, and the smoothing effect
of integration is stronger.
Therefore, its resolution is lower than
that of normal sampling.
.For the former, the integral interval is larger, and the smoothing effect
of integration is stronger.
Therefore, its resolution is lower than
that of normal sampling.
The substepped sequence is a moving-sum of the normal-sampled sequence. For instance, the pixel value at x=1 in Figure 1C comes from the pixel value at x=1 in A, which is equal to the sum of the pixel values at x=0, 1 in D.
The moving-sum operation is, in fact, a cross-correlation of the normal-sampled sequence with the kernel kc(n) (Figure 1E). However, this cross-correlation is equivalent to a convolution with the kernel k(n), k(n)=kc(-n). Therefore, deconvolution of the substepped sequence with respect to the kernel k(n) can be carried out to reconstruct the normal-sampled sequence. As a result, the smoothing effect due to the moving-sum is eliminated and resolution is improved.
In summary, when the pixel size is too large, substepping in data acquisition can be employed to eliminate aliasing. The resulting N sequences from N channels are interlaced. This operation alone can improve resolution. However, the improvement in resolution is made mostly by deconvolution of the substepped sequence with respect to the kernel k(n) to eliminate the moving-sum effect in substepping, i.e., to weaken the smoothing effect of the integration operation.Deconvolution with respect to the PSF (Sect. 2.1.), which can be used to improve resolution (restore a0(x) from a(x)), is independent of reconstruction of substepped data.
Undersampling with WFPC2 occurs because of the large pixel size of the CCD chips. The substepping technique used to overcome this problem is named ``subpixel dithering'' or simply ``dithering'' (Figure 2a).
During an observation, the pointing of the telescope is changed so that successive images are shifted along each axis by subpixel amounts. Then, these images are combined to obtain a single image having a smaller pixel size on a finer grid, using the POCS-based method (Adorf 1995), ``Drizzling'' method (Hook & Fruchter 1997), and deconvolution-based methods like acoadd, crcoad, mem, and lucy in IRAF/STSDAS.
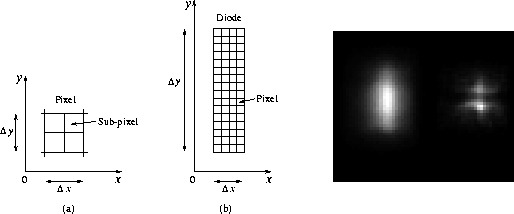
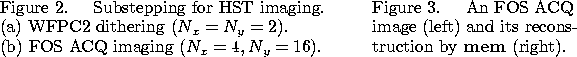
The undersampling problem with FOS arises from the large size of the diodes used for data acquisition. In substepping (Figure 2b), the step of the diode's motion is one quarter of its width in the X-direction, and one sixteenth of its height in the Y-direction.
The diode and the 64 (![]() ) small areas on it
would normally be called the pixel and subpixels, respectively, according to
standard substepping terminology.
However, in this particular case the small areas
have commonly, but inaccurately, become known as pixels.
) small areas on it
would normally be called the pixel and subpixels, respectively, according to
standard substepping terminology.
However, in this particular case the small areas
have commonly, but inaccurately, become known as pixels.
The deconvolution with respect to k(nx,ny) is called reconstruction. The deconvolution task mem or lucy, or the direct inversion task tarestore, in IRAF/STSDAS can be used for this purpose. tarestore results in high level sidelobes (rings) and noise in reconstructed images; mem and lucy give much better results (Wu & Caldwell 1997).
The smoothing effect due to the large diode size badly reduces resolution in FOS ACQ images. Reconstruction can remove this effect and dramatically improve resolution. Figure 3 shows an image, before and after reconstruction, of a star behind the bar in an FOS barred aperture.
In NICMOS imaging, PSFs are critically
sampled at ![]() and 1.75
and 1.75 ![]() m for Cameras 1 and 2, respectively.
When a working wavelength is shorter than
m for Cameras 1 and 2, respectively.
When a working wavelength is shorter than ![]() , the problem of
undersampling occurs. The situation here is similar to WFPC2 in principle.
Therefore, the substepping technique can be used.
, the problem of
undersampling occurs. The situation here is similar to WFPC2 in principle.
Therefore, the substepping technique can be used.
Adorf, H.-M. 1995, in Astronomical Data Analysis Software and Systems IV, A.S.P. Conf. Ser., Vol. 77, eds. R. A. Shaw, H. E. Payne & J. J. E. Hayes (San Francisco: ASP), 456
Hook, R. N. & Fruchter, A. S. 1997, in Astronomical Data Analysis Software and Systems VI, A.S.P. Conf. Ser., Vol. 125, eds. G. Hunt & H. E. Payne (San Francisco: ASP), 147
Wu, N. & Caldwell, J. 1997, in Proceedings of 1997 HST Calibration Workshop, Space Telescope Science Institute, ed. S. Casertano, et al. (in press)
Next: The Co-Addition Technique Applied to Images of Galaxy Cores
Up: Applications
Previous: Slitless Multiobject Spectroscopy with FOSC Type Instruments
Table of Contents -- Index -- PS reprint -- PDF reprint