



 112 kB PostScript reprint
112 kB PostScript reprint
Next: An Approach for
Up: Data Modeling and
Previous: Application of the
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
J.-P. De Cuyper and H. Hensberge
Koninklijke Sterrenwacht van België, Ringlaan 3, B-1180 Brussel,
België
Abstract:
Unrecognized blending in Thorium-Argon (Th-Ar) lamp spectra is a main contributor to
calibration uncertainties. We present improved dispersion-dependent Th-Ar
wavelengths for the features seen with moderate dispersion instruments.
The calibration of astrophysical spectra in wavelength based
on calibration lamp data suffers from different kinds of
uncertainties. Besides inaccuracies in the observational
phase, common data reduction practice adds
``pixelation'' errors, due to the fact that the centering method does not use
the correct PSF. These model mismatch errors depend, for a given feature, on
the sub-pixel location of the line center (David & Verschueren, private
communication). In addition, there are dispersion-dependent errors, due to
the fact that the laboratory input wavelengths refer to a pure line, while the
features observed at astrophysical dispersions are generally blended to
some extent. This aspect is the subject of our paper, with an application to
Th-Ar lamps. Lastly, there is a lack of robustness by using a calibration
relation with too many
parameters with respect to the physics involved: echelle orders are often
fitted independently, as well as sequences of spectra obtained under similar
conditions (Hensberge & Verschueren 1989; Hensberge et al. 1995).
Following T. M. Brown (1990), the centering accuracy for critically sampled
Gaussian lines in the photon-noise limit is 0.01 pixel for lines with 3400
electrons detected in their central pixel (after extraction in cross-order
direction). Usually as there are enough calibration lines available,
the systematic effects on the centering and on the input data should not exceed
this level.
Therefore, even fairly weak blends cannot be included as calibrators
without correcting their laboratory wavelength (Hensberge & Verschueren
1990). Figure 1 shows six lines,
five of which are discretizations of a Gaussian PSF with 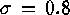 .
One of them is actually a blend with a line having 10% of the
intensity of the primary and situated one pixel to the right of the primary.
The blend induces an error of 0.07 pixel compared to the wavelength of
the primary line. The heavily blended lines commonly eliminated by observers
correspond to substantially larger errors.
.
One of them is actually a blend with a line having 10% of the
intensity of the primary and situated one pixel to the right of the primary.
The blend induces an error of 0.07 pixel compared to the wavelength of
the primary line. The heavily blended lines commonly eliminated by observers
correspond to substantially larger errors.
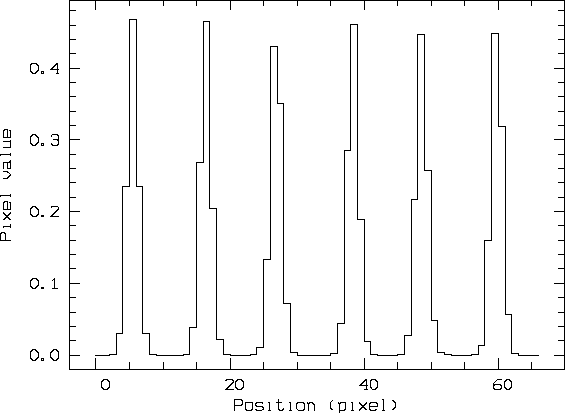
Figure: Shows five discretizations of a Gaussian line indistinguishable from
a weak blend feature.
Original PostScript figure (11 kB)
Unblended lines are quite scarce at moderate dispersion.
However, accurate calibration points can be provided by the many weakly blended
lines if their input wavelengths are corrected for blending.
Computations were done at four pixel scales between 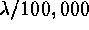 and
lines. The laboratory spectra were broadened to the desired resolution in
order to determine the dispersion-dependent input wavelength of the features.
The uncertainties present are due to several factors, such as
the relative line intensities, the line width, the exact centering algorithm
etc., and the details of the computations are discussed in De Cuyper &
Hensberge (1995).
and
lines. The laboratory spectra were broadened to the desired resolution in
order to determine the dispersion-dependent input wavelength of the features.
The uncertainties present are due to several factors, such as
the relative line intensities, the line width, the exact centering algorithm
etc., and the details of the computations are discussed in De Cuyper &
Hensberge (1995).
The laboratory data were taken from Palmer et al. (1983)
for Th and of Minnhagen (1973) and Norlèn (1973) for Ar.
The Ar to Th line ratios used are compatible with the lamps in use at ESO
The spectrum was synthesized
over a seven pixel wide
interval for 20 different discretizations (shifted in steps of 0.05 pixel).
The centering algorithm applied fits a Gaussian + constant. Improved
wavelengths were derived for the features showing small (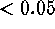 pixel) and
stable (RMS over all discretizations
pixel) and
stable (RMS over all discretizations 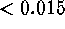 pixel) corrections.
pixel) corrections.
We have composed input line lists at four pixel scales for direct use,
containing a selection of commonly detectable, useful lines and their
corrected wavelengths. In addition, a list containing the complete information
and an algorithm permitting interpolation to other pixel sizes is provided.
(For information see the MIDAS-KSB-ORB Home Page.)
P. Ballester is kindly acknowledged for making these lists publicly available
through the ESO facilities (see the ESO Home Page).
Table 1 summarizes the acceptance statistics. Figure 2 gives an example of the
useful calibrators in an order of a CASPEC spectrum. When aiming for the
highest possible accuracy, it is advisable to use more stringent criteria
than those set in the computations. Moreover, this costs
only a few of the selected lines.
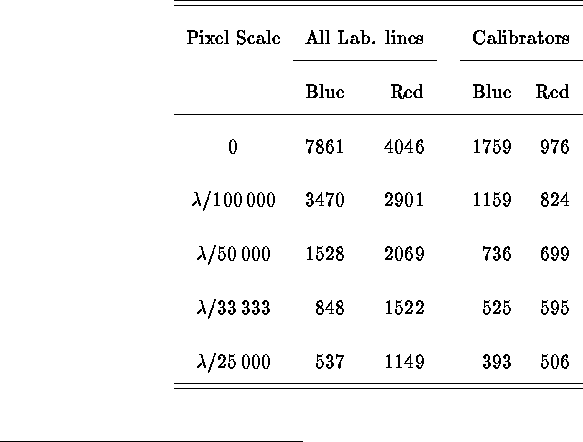
Table: Statistics of useful calibrators for two wavelength intervals
( 550nm),
including all lines and those measurable with sufficient accuracy.
550nm),
including all lines and those measurable with sufficient accuracy.
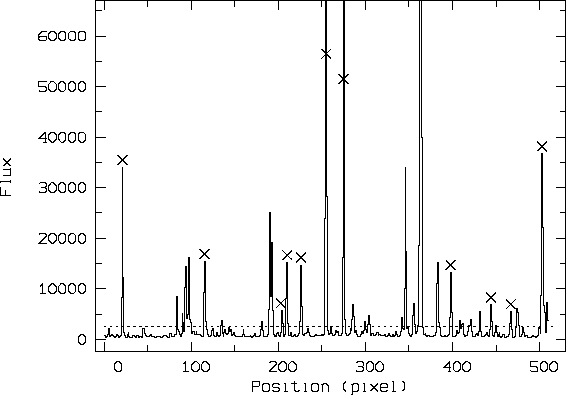
Figure: Shows an order (417--423nm)
from a CASPEC spectrum (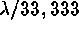 ). The useful calibrators lying above
the indicated level (
). The useful calibrators lying above
the indicated level ( line) are marked with an x sign.
Original PostScript figure (27 kB)
line) are marked with an x sign.
Original PostScript figure (27 kB)
Residuals of observed line positions with respect to calibration fits are in
general still dominated by erroneous assumed laboratory wavelengths even after
removal of the visually apparent blends or the apparent outliers. The
introduction of dispersion-dependent wavelengths for the many weakly
blended features at moderately high dispersion permits one to get the
residuals considerably lower, to a few hundredths of a pixel. The wavelength
corrections were obtained independently from the calibration
fitting procedure, in contrast to clipping algorithms applied on
residuals relative to such a relation. As a consequence, we can provide
more realistic input wavelengths for Th-Ar lamps from below 300 to over
1000nm in the dispersion range of interest.
Better input data not only lead directly to more precise calibration
coefficients, but also provide the opportunity to derive a more
appropriate mathematical representation for the calibration relation.
Adequate results can then be obtained by few-parameter fits, which
in the case of echelle spectroscopy cannot be represented as
bivariate polynomials. The order dependence needs to be expressed as
a ratio of two linear functions of the order number (Hensberge & Verschueren
1989).
Acknowledgments:
This research work was carried out in the framework of the project `Service
Centers and Research Networks' initiated and financed by the Belgian Federal
Scientific Services (DWTC/SSTC) under contract number SC/005. The analysis
profited from experience with calibration data taken
during several runs at the European Southern Observatory; with the echelle
spectrographs ECHELEC at the 1.5m telescope, and CASPEC at the 3.6m
telescope. We acknowledge the observers A. G. A. Brown, E. J. de Geus,
R. S. Lepoole and, in particular, W. Verschueren who was, in addition,
deeply involved in the data reduction. H. Van Diest is thanked for computer
assistance.
References:
Brown, T. M. 1990, in CCD's in Astronomy, ASP Conf. Ser., Vol. 8,
ed. G. H. Jacoby (San Francisco, ASP), p. 335
De Cuyper, J.-P., & Hensberge, H. 1995, A&A, in preparation
Hensberge, H., & Verschueren, W. 1989, ESO Messenger, 58, 51
Hensberge, H., & Verschueren, W. 1990, in Errors, Bias and
Uncertainties in Astronomy, eds. F. Murtagh & C. Jaschek (Cambridge,
Cambridge Univ. Press), p. 335
Hensberge, H., Verschueren, W., & De Cuyper, J.-P. 1995, A&A,
in preparation
Minnhagen, L. 1973, J. Opt. Soc. Amer., 63, 1185
Norlèn G. 1973, Physica Scripta, 8, 249
Palmer, B. A., & Engleman, R. Jr. 1983, in Atlas of the
Thorium Spectrum, ed. H. Sinoradzky (Los Alamos, Los Alamos National
Laboratory)




 112 kB PostScript reprint
112 kB PostScript reprint
Next: An Approach for
Up: Data Modeling and
Previous: Application of the
adass4_editors@stsci.edu
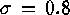 .
One of them is actually a blend with a line having 10% of the
intensity of the primary and situated one pixel to the right of the primary.
The blend induces an error of 0.07 pixel compared to the wavelength of
the primary line. The heavily blended lines commonly eliminated by observers
correspond to substantially larger errors.
.
One of them is actually a blend with a line having 10% of the
intensity of the primary and situated one pixel to the right of the primary.
The blend induces an error of 0.07 pixel compared to the wavelength of
the primary line. The heavily blended lines commonly eliminated by observers
correspond to substantially larger errors.

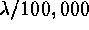 and
lines. The laboratory spectra were broadened to the desired resolution in
order to determine the dispersion-dependent input wavelength of the features.
The uncertainties present are due to several factors, such as
the relative line intensities, the line width, the exact centering algorithm
etc., and the details of the computations are discussed in De Cuyper &
Hensberge (1995).
and
lines. The laboratory spectra were broadened to the desired resolution in
order to determine the dispersion-dependent input wavelength of the features.
The uncertainties present are due to several factors, such as
the relative line intensities, the line width, the exact centering algorithm
etc., and the details of the computations are discussed in De Cuyper &
Hensberge (1995).
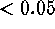 pixel) and
stable (RMS over all discretizations
pixel) and
stable (RMS over all discretizations 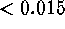 pixel) corrections.
pixel) corrections.

 550nm),
including all lines and those measurable with sufficient accuracy.
550nm),
including all lines and those measurable with sufficient accuracy.
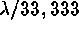 ). The useful calibrators lying above
the indicated level (
). The useful calibrators lying above
the indicated level ( line) are marked with an x sign.
line) are marked with an x sign.