Next: Restoration of Digitized Astronomical Plates with the Pixon Method
Up: Algorithms
Previous: Adaptive Optics Software on the CfAO Web Page
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
Greisen, E. G., Valdes, F. G., Calabretta, M. R., & Allen, S. L. 2003, in ASP Conf. Ser., Vol. 295 Astronomical Data Analysis Software and Systems XII, eds. H. E. Payne, R. I. Jedrzejewski, & R. N.
Hook (San Francisco: ASP), 403
Representations of Spectral Coordinates in FITS
Eric W. Greisen1
National Radio Astronomy Observatory, P. O. Box O, Socorro, NM
87801 USA; Email: egreisen@nrao.edu
Francisco G. Valdes2
National Optical Astronomy Observatories, P. O. Box 26732,
Tucson, AZ 85719 USA; Email: valdes@noao.edu
Mark R. Calabretta3
Australia Telescope National Facility, P. O. Box 76, Epping,
NSW 1710 Australia; Email: Mark.Calabretta@atnf.csiro.au
Steven L. Allen4
UCO/Lick Observatory, University of California, Santa Cruz, CA
95064 USA; Email: sla@ucolick.org
Abstract:
In Paper I, Greisen & Calabretta (2003) describe a generalized method
for specifying the coordinates of FITS data samples. Following that
general method, Calabretta & Greisen (2003) in Paper II describe
detailed conventions for defining celestial coordinates as they are
projected onto a two-dimensional plane. The present paper extends the
discussion to the spectral coordinates of wavelength, frequency, and
velocity. World coordinate functions are defined for spectral axes
sampled evenly in wavelength, frequency, or velocity, evenly in the
logarithm of wavelength or frequency, as projected by ideal dispersing
elements, and as specified by a lookup table. Papers I and II have
been accepted into the FITS standard by the North American, Japanese
and European FITS Committees; we expect the present work to be
accepted as well. The full text of the proposed standards can be
found at
http://www.aoc.nrao.edu/~egreisen.
Greisen & Calabretta (2003, ``Paper I'') describes the computation
of the world or physical coordinates as a multi-step process. The
vector of pixel offsets from the reference point is multiplied by a
linear transformation matrix and then scaled to physical units.
Mathematically, this is given by
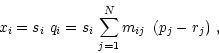 |
(1) |
where 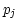 are pixel coordinates,
are pixel coordinates, 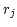 are pixel
coordinates of the reference point given by CRPIX
are pixel
coordinates of the reference point given by CRPIX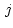 ,
,
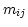 is a linear transformation matrix given either by
PC
is a linear transformation matrix given either by
PC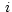 _
_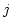 or CD
or CD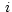 _
_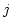 ,
, 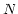 is the dimensionality of the
WCS representation given by WCSAXES, and
is the dimensionality of the
WCS representation given by WCSAXES, and 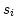 is a scaling
given either by CDELT
is a scaling
given either by CDELT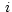 or by 1.0. The final step in the
computation is the conversion of these linear relative coordinates
into the actual physical coordinates. The conventions to be applied
to ideal spectral axes are described in ``Paper III'' (Greisen et al. 2003) and summarized here. A later work (Calabretta, et al. 2003,
``Paper IV'') will address the corrections needed to convert real
astronomical data into the ideal axes assumed in the celestial
coordinates (Calabretta & Greisen 2003, ``Paper II'') and present
manuscripts.
or by 1.0. The final step in the
computation is the conversion of these linear relative coordinates
into the actual physical coordinates. The conventions to be applied
to ideal spectral axes are described in ``Paper III'' (Greisen et al. 2003) and summarized here. A later work (Calabretta, et al. 2003,
``Paper IV'') will address the corrections needed to convert real
astronomical data into the ideal axes assumed in the celestial
coordinates (Calabretta & Greisen 2003, ``Paper II'') and present
manuscripts.
The basic ``spectral'' coordinates are frequency, wavelength, and
Doppler relativistic velocity. There are several other coordinates
which are proportional to one of these, including wavenumber, energy,
and ``radio'' and ``optical'' conventional velocities. Let us
consider the case in which an axis is linearly sampled in spectral
variable 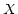 , but is to be expressed in terms of variable
, but is to be expressed in terms of variable 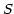 . We may
restrict
. We may
restrict 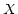 to the basic types since all others are linearly
proportional to one of them. Let us also introduce an intermediate
variable
to the basic types since all others are linearly
proportional to one of them. Let us also introduce an intermediate
variable 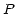 which is the basic variable associated with
which is the basic variable associated with 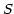 . The
relationship between
. The
relationship between 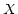 and
and 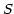 is then
is then
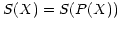 with inverse
with inverse
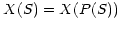 . The statement that an axis is linearly sampled in
. The statement that an axis is linearly sampled in
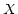 simply means that
simply means that
 |
(2) |
where  is the intermediate value
is the intermediate value 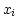 for the spectral axis and
for the spectral axis and
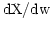 is a constant. Since, to first order
and very near the reference point, the axis is linear in
is a constant. Since, to first order
and very near the reference point, the axis is linear in 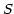 , i.e.,
, i.e.,
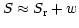 , we may determine the derivative by
, we may determine the derivative by
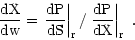 |
(3) |
A three-step algorithm chain is then indicated:
- Compute once
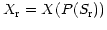 and
and
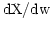 using Equation (3) and then compute
using Equation (3) and then compute 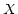 at
at 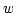 using
Equation (2).
using
Equation (2).
- Compute
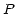 from
from 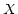 using the set of non-linear relationships
between the basic spectral coordinates..
using the set of non-linear relationships
between the basic spectral coordinates..
- Compute
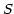 from
from 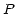 using the set of linear relationships
between the basic and secondary spectral coordinates.
using the set of linear relationships
between the basic and secondary spectral coordinates.
Dispersion coordinates for UV, optical, and IR spectra at 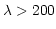 nm are commonly given as wavelengths in air rather than in
vacuum. The relationship between these is given by
nm are commonly given as wavelengths in air rather than in
vacuum. The relationship between these is given by
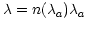 and causes a relative difference of around
0.03%. The conversion between wavelengths in air and wavelengths in
vacuum adds another step in the chain described above.
and causes a relative difference of around
0.03%. The conversion between wavelengths in air and wavelengths in
vacuum adds another step in the chain described above.
Paper III presents a full set of codes to be used in keyword
CTYPE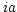 for spectral coordinate types and for the non-linear
algorithms involved, including air wavelengths. Keywords
RESTFRQ
for spectral coordinate types and for the non-linear
algorithms involved, including air wavelengths. Keywords
RESTFRQ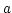 and RESTWAV
and RESTWAV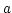 are reserved to give the line rest
frequency (in Hz) or wavelength (in m) needed for the conversion
between frequency/wavelength and velocity.
are reserved to give the line rest
frequency (in Hz) or wavelength (in m) needed for the conversion
between frequency/wavelength and velocity.
Figure 1:
Geometry of gratings, prisms, and grisms. This simplified
representation omits the collimation and focusing optics.
Dashed lines mark ray paths in the plane of the figure - the
``dispersion plane''. The normal to the grating/exit prism
face and the normal to the detector plane are each projected
onto the dispersion plane, and angles 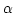 ,
, 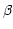 , and
, and
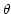 are measured with respect to these projected normals.
Usually the incident ray for a prism or grism is perpendicular
to the entry face so that
are measured with respect to these projected normals.
Usually the incident ray for a prism or grism is perpendicular
to the entry face so that 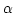 is equal to the prism angle,
is equal to the prism angle,
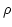 . Angle
. Angle 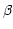 is wavelength-dependent, and
consequently so is the offset
is wavelength-dependent, and
consequently so is the offset 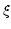 in the dispersion direction
on the detector. The intermediate spectral world coordinate,
in the dispersion direction
on the detector. The intermediate spectral world coordinate,
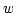 , is proportional to
, is proportional to 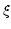 . Reference wavelength
. Reference wavelength
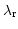 follows the reference ray defined by
follows the reference ray defined by
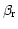 and illuminates the reference point at
and illuminates the reference point at
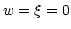 . The normal to the detector plane is shown tilted by
angle
. The normal to the detector plane is shown tilted by
angle 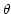 from the reference ray though typically this
angle is zero. The grating spacing
from the reference ray though typically this
angle is zero. The grating spacing 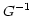 is indicated.
is indicated.
 |
One common form of spectral data is produced by imaging the light from
a disperser, such as a prism, grating, or grism, as illustrated in
Figure 1. Paper III presents the full mathematics by
which the wavelength 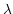 and the spacing at the detector
and the spacing at the detector
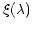 may be related. The basic grism equation is given by
may be related. The basic grism equation is given by
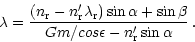 |
(4) |
Despite numerous approximations made in the development of the
mathematics, it is found that suitable parameters provide good fits to
a variety of spectrometers in use at the KPNO.
There are numerous instances in which a physical coordinate is well
defined at each pixel along an image axis, but the relationship of the
coordinate values between pixels
cannot be described by a simple functional form.
Observations of the same object made at an arbitrary set of
frequencies or times are the simplest examples. In addition,
the calibration of some spectrographs is represented best by a list of
wavelengths for each pixel on the spectral axis.
Fully separable, one-dimensional axes of this type may be represented
by an algorithm, -TAB, defined in Paper III. A FITS binary
table containing only one row is used. The coordinates are given by a
vector of values in a single cell, optionally accompanied by a second
indexing vector in a second cell within the row. The parameters
required by -TAB are the table extension name, the table version
number, the table level number, the column name for the coordinate
vector, and the column name for the optional indexing vector. The
character-valued generic keyword PS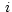 _
_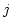 is introduced to
provide the three character-valued parameters of this algorithm. The
coordinate value is found by first evaluating Equation (1) and
adding the reference value. The result is used as a value to be
looked up in the vector of values found in the indexing vector cell. The
corresponding position in the vector of values in the coordinate
vector cell then provides the actual coordinate. If the indexing vector
is omitted, the value found with Equation (1) is used as a
direct index for the coordinate vector.
is introduced to
provide the three character-valued parameters of this algorithm. The
coordinate value is found by first evaluating Equation (1) and
adding the reference value. The result is used as a value to be
looked up in the vector of values found in the indexing vector cell. The
corresponding position in the vector of values in the coordinate
vector cell then provides the actual coordinate. If the indexing vector
is omitted, the value found with Equation (1) is used as a
direct index for the coordinate vector.
The -TAB algorithm described above is then generalized to cases
in which the coordinates on 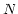 axes are dependent on each other, but
the indexing vectors are independent. In this case, the values of the
coordinates are contained in one column of the (one-row) table as an
array of dimensions
axes are dependent on each other, but
the indexing vectors are independent. In this case, the values of the
coordinates are contained in one column of the (one-row) table as an
array of dimensions
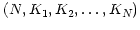 , where
, where 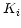 is the
number of indexing values on axis
is the
number of indexing values on axis 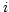 . The indexing vector for axis
. The indexing vector for axis
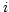 , if present, will occupy a separate column and will contain
, if present, will occupy a separate column and will contain 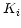 values in a one-dimensional array. An additional parameter is
required for each of the
values in a one-dimensional array. An additional parameter is
required for each of the 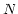 coordinates to give the axis number
coordinates to give the axis number 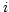 within the coordinate array.
within the coordinate array.
Paper I has defined a general framework to describe world coordinates
in the FITS format; Paper II has extended that framework to
describe ideal celestial coordinate representations. Paper III,
summarized here, extends the discussion to ideal spectral coordinates
and introduces a general table lookup algorithm. All three papers
are well on their way to becoming part of the IAU FITS Standard.
References
Calabretta, M. R. et al. 2003, Representations of
distortions in FITS world coordinate systems, in preparation,
(``Paper IV'')
Calabretta, M. R. & Greisen, E. W. 2003, A&A, accepted
(``Paper II'')
Greisen, E. W. & Calabretta, M. R. 2003, A&A, accepted
(``Paper I'')
Greisen, E. W., Valdes, F. G., Calabretta, M. R., & Allen, S. A. 2003, A&A, in preparation (``Paper III'')
Footnotes
- ... Greisen1
- The National Radio Astronomy Observatory is a
facility of the (U.S.) National Science Foundation operated under
cooperative agreement by Associated Universities, Inc.
- ... Valdes2
- The National Optical Astronomy Observatory is a
facility of the (U.S.) National Science Foundation operated under
cooperative agreement by Associated Universities for Research in
Astronomy, Inc.
- ... Calabretta3
- The Australia Telescope is funded by the Commonwealth
of Australia for operation as a National Facility managed by CSIRO.
- ... Allen4
- UCO/Lick Observatory is operated by the University of
California.
© Copyright 2003 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: Restoration of Digitized Astronomical Plates with the Pixon Method
Up: Algorithms
Previous: Adaptive Optics Software on the CfAO Web Page
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
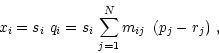
![]() , but is to be expressed in terms of variable
, but is to be expressed in terms of variable ![]() . We may
restrict
. We may
restrict ![]() to the basic types since all others are linearly
proportional to one of them. Let us also introduce an intermediate
variable
to the basic types since all others are linearly
proportional to one of them. Let us also introduce an intermediate
variable ![]() which is the basic variable associated with
which is the basic variable associated with ![]() . The
relationship between
. The
relationship between ![]() and
and ![]() is then
is then
![]() with inverse
with inverse
![]() . The statement that an axis is linearly sampled in
. The statement that an axis is linearly sampled in
![]() simply means that
simply means that
![]() nm are commonly given as wavelengths in air rather than in
vacuum. The relationship between these is given by
nm are commonly given as wavelengths in air rather than in
vacuum. The relationship between these is given by
![]() and causes a relative difference of around
0.03%. The conversion between wavelengths in air and wavelengths in
vacuum adds another step in the chain described above.
and causes a relative difference of around
0.03%. The conversion between wavelengths in air and wavelengths in
vacuum adds another step in the chain described above.
![]() for spectral coordinate types and for the non-linear
algorithms involved, including air wavelengths. Keywords
RESTFRQ
for spectral coordinate types and for the non-linear
algorithms involved, including air wavelengths. Keywords
RESTFRQ![]() and RESTWAV
and RESTWAV![]() are reserved to give the line rest
frequency (in Hz) or wavelength (in m) needed for the conversion
between frequency/wavelength and velocity.
are reserved to give the line rest
frequency (in Hz) or wavelength (in m) needed for the conversion
between frequency/wavelength and velocity.

![]() and the spacing at the detector
and the spacing at the detector
![]() may be related. The basic grism equation is given by
may be related. The basic grism equation is given by
![]() _
_![]() is introduced to
provide the three character-valued parameters of this algorithm. The
coordinate value is found by first evaluating Equation (1) and
adding the reference value. The result is used as a value to be
looked up in the vector of values found in the indexing vector cell. The
corresponding position in the vector of values in the coordinate
vector cell then provides the actual coordinate. If the indexing vector
is omitted, the value found with Equation (1) is used as a
direct index for the coordinate vector.
is introduced to
provide the three character-valued parameters of this algorithm. The
coordinate value is found by first evaluating Equation (1) and
adding the reference value. The result is used as a value to be
looked up in the vector of values found in the indexing vector cell. The
corresponding position in the vector of values in the coordinate
vector cell then provides the actual coordinate. If the indexing vector
is omitted, the value found with Equation (1) is used as a
direct index for the coordinate vector.
![]() axes are dependent on each other, but
the indexing vectors are independent. In this case, the values of the
coordinates are contained in one column of the (one-row) table as an
array of dimensions
axes are dependent on each other, but
the indexing vectors are independent. In this case, the values of the
coordinates are contained in one column of the (one-row) table as an
array of dimensions
![]() , where
, where ![]() is the
number of indexing values on axis
is the
number of indexing values on axis ![]() . The indexing vector for axis
. The indexing vector for axis
![]() , if present, will occupy a separate column and will contain
, if present, will occupy a separate column and will contain ![]() values in a one-dimensional array. An additional parameter is
required for each of the
values in a one-dimensional array. An additional parameter is
required for each of the ![]() coordinates to give the axis number
coordinates to give the axis number ![]() within the coordinate array.
within the coordinate array.